Année 2025-2026:
Semaine 17 du lundi 2 Février : endomorphismes d’un espace euclidien Un cours très riche qui demande un travail en profondeur :- Définition de l’adjoint, écriture matricielle en b.o.n.
- Si F est un s.e.v. stable par u alors son orthogonal est stable par u*.
- Donner le plus de caractérisations possibles des isométries vectorielles avec dém de l’une d’elles au choix des colleurs..
- Donner le plus de caractérisations possibles des matrices orthogonales : attention déterminant =+- 1 n’est PAS une caractérisation de ces matrices !
- Montrer qu’une matrice orthogonale symétrique est une matrice de symétrie orthogonale et montrer que vous avez compris ce que chaque terme de cette phrase veut dire….
- Théorème spectral sur les endomorphismes auto adjoints : preuve par récurrence sur la dimension (sans prouver tous les lemmes utilisés ou démo au choix parmi ces lemmes).
- Pour f dans L(E), forme bilinéaire associée (x,y)-> (x|f(y)). Par définition f est auto adjoint ssi cette forme bilinéaire est symétrique f et forme quadratique associée x-> (x|f(x)). Ecriture de ces deux objets en coordonnée dans une b.o.n. quelconque.
- Ecriture de la forme quadratique x-> (f(x)|x) dans une b.o.n. de dz. de f auto adjoint , application à une caractérisation de la plus grande et de la plus petite v.p. de f.
- Définition des autoadjoints positifs (resp. matrices symétriques positives) et caractérisation par le spectre.
- Démonstration matricielle de la forme de matrices de O_2(R)
- Théorème de réduction des isométries vectorielles en dimension n : idées de la preuve en admettant les lemmes clefs (tous assez simples à montrer par ailleursn pas besoin de formaliser la récurrence pour les blocs de rotation)
- Justifier que pour X'(t)=A.X(t) avec A matrice indép. de t, les solutions sont les fonctions t->e^{tA} C.
- Généralisation du point précédent. Forme des solutions pour X'(t)=A.X(t)+B(t) avec une intégrale.
- Enoncé précis du théorème de Cauchy Lipschitz linéaire pour les systèmes X'(t)=A(t)X(t)+B(t), conséquences pour la structure de l’ensemble des solutions dans les cas homogène et non homogène.
- Traduction du théorème dans le cas des EDL scalaires d’ordre n (vectorialisation).
- Définition du Wronskien de deux solutions d’une EDL scalaire d’ordre 2, et E.D. vérifiée par celui-ci
- Méthode de variations des constantes seulement dans le cas d’ordre au plus 2.
- Résolution d’un système linéaire X'(t)=A.X(t) avec A matrice constante 2×2 ou 3×3:
- Cas où A est diagonalisable dans R
- Cas où A est diagonalisable dans C et qu’on veut des solutions réelles
- Cas où A est seulement trigonalisable : on a donné deux méthodes
- la méthode d’une simple trigonalisation suivie d’une résolution « de bas en haut » par substitution,
- le calcul de exp(tT) dans le cas simple où T=lambda I+ N autrement dit T n’a qu’une seule v.p. (ceci se généralise par bloc avec les sev caractéristiques mais on n’a pas traité d’autres exemples).
- Résolution d’équations différentielles linéaires scalaires d’ordre deux :
- Méthodes de première année : déjà révisées la semaine dernière, toujours d’actualité !
- Méthode de la variation Des constantes pour les ED d’ordre deux : à bien maîtriser.
- Quand on ne connaît pas de solutions de l’équation homogène : exemple de recherche des solutions D.S.E. (pratique à bien maîtriser !)
- Quand on connaît une solution de l’équation homogène et qu’on en vu une autre indépendante, technique de la réduction de l’ordre par variation de la constante.
- la dérivation et l’intégration des fonctions d’une variable réelle à valeurs vectorielles, questions de cours possibles
-
-
-
- Trois définitions équivalentes de la dérivabilité pour f : I -> E (dém. non demandée)
- Dérivée de L o f si f est dérivable de I dans E et L est linéaire de E dans F (dém.)
- Dérivée de B(f,g) si f (resp. g) sont dérivables de I dans E (resp. dans F) et B : E x F-> G est bilinéaire (dém.)
- Extension du point précédent aux applications n-linéaires (typiquement déterminant) (pas de dém. juste la formule)
- T.A.F. généralisé à deux fonctions » f'(c) (g(b)-g(a))=g'(c)(f(b)-f(a)) » démonstration vectorielle
- Dérivation de t-> exp(tA) par théorème de dérivation terme à terme à valeurs vectorielles (dém non détaillée mais à travailler !).
- Inégalité triangulaire pour les intégrales de fonctions vectorielles (démonstration avec les sommes de Riemann) et application à l’I.A.F. dans l’hypothèse C^1.
- Pourquoi le théorème de Rolle (et donc l’égalité des A.F.) sont ils faux dans le cas des fonctions à valeurs vectorielles non scalaires?
- Formules de Taylor à savoir parfaitement : DU SOIN POUR l’énoncé des théorèmes ! Pas juste la formule mais hypothèses de régularités précises.
-
-
-
- Les révisions sur les équations différentielles de première année :
-
-
- résolution concrète d’E.D.linéaires du premier ordre avec la méthode de variation de la constante : les exercices 8,9,10 abordent les problèmes de raccords pour les équations différentielles singulières, c’est l’occasion aussi de révision sur les développement limités pour les raccords et bien sûr des calculs de primitives !
- des exercices plus théoriques sur le 1er ordre où l’on voit que la M.V.C. permet une écriture plus abstraite des solutions, qui aboutit à des propriétés précises de ces solutions.
- enfin des EDL du second ordre à coefficient constant avec second membres gentils : polynôme x exponentielle x cos ou sin. On a révisé les cas de résonance où la solution particulière n’est pas de la même forme que le second membre car celui ci correspond déjà au régime libre.
-
-
- version à variable continue du théorème de convergence dominée,
- théorème de continuité pour les intégrales à paramètres
- théorème sur le caractère C^k des intégrales à paramètres
- Continuité de la TF (transformée de Fourier) d’une fonction intégrable
- Continuité sur ]0,+oo[ de la TL (transformée de Laplace) d’une fonction c.p.m. bornée, extension à la variable complexe.
- Théorème de la valeur initiale pour la transformée de Laplace dans le cas facile d’une fonction bornée : L(f)(x)=f(0)/x+ o(1/x) quand x–>+oo.
- Lemme de Riemann-Lebesgue dans le cas facile où f est de classe C^1 et f et f’ sont intégrables : F(f)(x) –>0 pour x–>+oo
- Caractère C^1 et dérivation de la TL du sinus cardinal sur l’ouvert ]0,+oo[ : application au calcul de cette Transformée.
- En bonus pour les plus à l’aise, continuité de cette TL en 0 (intégrale semi-convergente, I.P.P pour se ramener au cadre de Lebesgue) et calcul de l’intégrale du sinus cardinal sur R¨^+.
- Calcul de la dérivée p-ième de la TF d’une fonction f telle que pour tout k=0,1,..p, la fonction t-> t^k f(t) doit intégrable. (Si ceci est vrai pour tout p, on dit que la fonction est « à décroissance rapide »).
- Etude complète de la fonction Gamma : notamment justification soigneuse du caractère C^k et justifications pour le tracé du graphe.
- REVOIR les techniques de calculs d’intégrales et de primitives (1ère année, planche I1).
- Bien savoir aussi dériver si x est dans les bornes des intégrales (1ère année… et pas que..)
- Lemme d’Abel, dém. et (prop.-)-définition du rayon de convergence.
- Test de d’Alembert pour les séries entières : dém. avec le lemme pour les séries numériques laissée en exercice en cours, mais faite sur les exemples des séries lacunaires ensuite en exercices !
- Prop. :
 ont même rayon de convergence (au programme officiel pour alpha=1, démontrée, pour pas plus cher pour alpha qcq donc je pense qu’on peut s’en servir pour alpha quelconque).
ont même rayon de convergence (au programme officiel pour alpha=1, démontrée, pour pas plus cher pour alpha qcq donc je pense qu’on peut s’en servir pour alpha quelconque). - Rayon de convergence d’une somme et produit de Cauchy.
- Continuité de la fonction somme dans le disque ouvert de convergence.
- Pour ce qui la variable est réelle :
- Théorème de continuité radiale d’Abel : énoncé seulement, mais savoir l’appliquer sur des exemples (série harmonique alternée…)
- Dérivation terme à terme automatique pour les sommes de séries entières
- unicité des coefficients du D.S.E., série de Taylor, rigidité des fonctions D.S.E.
- DSE des fonctions usuelles : preuve de la formule du binôme (1+x)^a pour a réel avec la méthode de l’E.D. ou avec une formule de Taylor au moins pour x>0.
- Banque CCINP cf haut de la planche. Planche-S3-2024-2025 Nous avons traités les exercices 1 à 9 et 11, 12, nous traiterons au moins jusqu’au 14.
- Définir le produit scalaire canonique de R^n, dans M_{m,n}(R) (deux expressions montrer qu’elles coïncident)
- Produit scalaire dans L^2,continue(I,R) (justifier la convergence des l’intégrale)
- Produit scalaire dans l^2(N,R) (justifier la convergence de la série… non détaillée en classe).
- Expliquer pourquoi le p.s. est une application bilinéaire CONTINUE (savoir la caractérisation des appli. bilinéaires continues).
- Montrer que l’orthogonal d’une partie dense est réduit à {0}. Application au ‘lemme des moments’ (Banque CCINP 48 même si le corrigé de la banque est formulé sans produit scalaire, voir la rédaction faite en classe !).
- Lemme de représentation de Riesz pour les formes linéaires d’un espace euclidien.
- Montrer que l’orthogonal d’une partie A de E est un s.e.v. fermé de E.
- Existence d’un supplémentaire orthogonal pour un s.e.v. de dim. finie d’un espace préhilbertien.
- Formule de calcul de la projection orthogonale quand on connait une base orthogonale de ce s.e.v. : application à l’exemple très important des sommes partielles de la série de Fourier de f.
- Le projeté orthogonal d’un vecteur v sur un sev F est l’unique vecteur de F qui minimise la distance entre v et les vecteurs de F.
- Mise en oeuvre de l’orthogonalisation de Gram-Schmidt sur des exemples.
- Citer très précisément les deux théorèmes d’intégration d’une limite (celui avec la CVU sur un segment vs le T.C.D. de Lebesgue) : lesquels sait-on démontrer 🙂 ?
- Donner un exemple d’une suite de fonctions (f_n) qui Converge Uniformément sur un intervalle I (non borné) vers une fonction f et telle que l’intégrale sur I des f_n ne converge PAS vers l’intégrale sur I de f (étalement de la bosse : un dessin peut suffire, une fois transformé en fonction affine par morceau).
- Application du T.C.D. avec des « bornes variables » exemple de la limite de
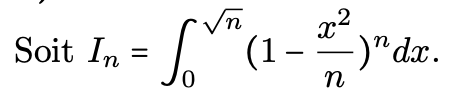
- Etude des intégrales de Wallis : détermination d’un équivalent. Toutes les étapes (relation de récurrence, invariant, encadrement) doivent être mémorisées.
- Méthode l’I.P.P fait sortir le terme prépondérant pour un équivalent, si f(1) non nul, de :
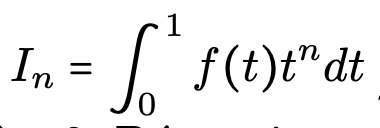
- Méthode l’I.P.P fait sortir le terme prépondérant pour un équivalent, si f(1) non nul, de :
- Le même équivalent par la méthode de changement de variable.
- Savoir qu’il y a dans le programme 3 théorèmes d’intégration terme à terme et savoir les citer !
- Intégration terme à terme d’une CVU sur un segment :
-
- application aux séries entières, comment obtenir le D.S.E. de ln(1+x) à partir de celui de 1/(1+x)
sur ]-1,1[.
- application à la formule donnant les coefficients a_n et b_n d’une série trigonométrique comme des intégrales sur sa somme (formule des coeff. de Fourier).
- application au calcul de l’intégrale de e^{it}/(a-e^{e^{it}} pour a dans C privé du cercle (indice de a par rapport au cercle)
- application aux séries entières, comment obtenir le D.S.E. de ln(1+x) à partir de celui de 1/(1+x)
-
- Théorème d’intégration terme à terme de Lebesgue en deux théorèmes : cas positif et cas signe quelconque. Donner des énoncés précis !
- Ce qu’on fait quand le théorème ne s’applique pas (notamment en cas de Cv par théorème des séries alternées spéciales).
- Planche I2 : Planche-I2-2025-2026, nous avons traités les exercices 1 à 5 (sauf le cas a>1 de l’ex 4 plus difficile) sur la convergence dominée et seulement 8 et 9 sur l’intégration terme à terme mais nous poursuivons en début de semaine sur l’intégration terme à terme.
- Lemme d’Abel, dém. et (prop.-)-définition du rayon de convergence.
- Lemme de d’Alembert pour les séries entières : dém. avec le lemme pour les séries numériques.
- Prop. ;
 ont même rayon de convergence (au programme officiel pour alpha=1, démontrée, pour pas plus cher pour alpha réel quelconque, démo « bonus » : ne pas pénaliser les étudiants que ne l’aurait pas bien maîtrisée en première semaine)
ont même rayon de convergence (au programme officiel pour alpha=1, démontrée, pour pas plus cher pour alpha réel quelconque, démo « bonus » : ne pas pénaliser les étudiants que ne l’aurait pas bien maîtrisée en première semaine) - Rayon de convergence d’une somme
- Produit de deux sommes de séries entières , produit de Cauchy des coefficients.
- Continuité de la fonction somme dans le disque ouvert de convergence (dém).
- Pour ce qui la variable est réelle :
- Dérivation terme à terme automatique à l’intérieur de l’intervalle de convergence pour les sommes de séries entières (dém !)
- unicité des coefficients du D.S.E., série de Taylor, rigidité des fonctions D.S.E. (dém.)
- application au caractère C^infini automatique de fonctions comme le sinus cardinal en 0.
- intégration et primitivation terme à terme automatique à l’intérieur de l’intervalle de Cv : application au D.S.E. de ln(1+x)
- théorème d’Abel radial (admis) ; savoir l’application pour montrer que la somme de la série harmonique alternée vaut ln(2).
- DSE des fonctions usuelles : preuve de la formule du binôme (1+x)^a pour a réel avec la méthode de l’E.D.
- On pourra demander un énoncé précis de théorème en début de colle.
- Démonstration du théorème de continuité d’une limite uniforme d’une suite de fonctions continues (idée importante « couper en trois » et attention à l’ordre des choix).
- Démonstration du théorème d’intégration d’une limite uniforme sur un segment.
- Le théorème d’interversion des limites a été admis : l’énoncé doit être bien restitué en version suite et en version séries (« sommation des limites »).
- Exemple de la fonction zeta réelle : plusieurs questions possibles : continuité, caractère C infini, limite à l’infini
- Cas où le théorème d’interversion des limites ne s’applique pas : comment montrer que zeta(x) tend vers l’infini quand x tend vers 1 avec la déf de la limite (question plus difficile bonus ci-dessous méthode plus simple avec l’équivalent).
- Exemple de la suite des fonctions x-> n sin(x/n) méthode pour la CVU sur les segments et pourquoi on n’ a pas CVU sur R
- Recherche d’équivalent de la somme d’une série de fonction :
- Méthode d’encadrement par des intégrales pour un équivalent quand x->1 de la fonction zeta (encore elle !)
- Méthode qui ramène à l’application du théorème d’interversion des limites en divisant par le candidat équivalent faite sur la somme des x/(n^a (1+nx^2))
- Exercice de la Planche-S2-2025-2026 : les ex 1 à 6 et 9 et 10 ont été traités et donnent déjà pas mal d’exemples de méthodes. On traitera sûrement 11 et 12 en début de semaine.
- Exercice de la banque CCINP ; il y en a beaucoup (cf. haut de la pl S2) : les élèves doivent en travailler au moins 4 pour cette semaine, leur demander ceux qu’ils ont travaillés.
- On commencera la colle par une étude d’intégrabilité de fonction à l’aide des théorèmes de comparaison : o, O, équivalents, majorations de l’intégrande .
- définitions et caractérisations de (au choix des colleurs) ouvert, fermé, adhérences, intérieurs…
- Montrer qu’une boule ouverte est ouverte.
- Montrer que l’adhérence d’une boule ouverte est la boule fermée
- Exercice : Montrer qu’un s.e.v. strict est d’intérieur vide.
- Caractérisation séquentielle des points adhérents.
- Lien complémentaire de l’adhérence/intérieur du complémentaire..
- Ouverts et fermés relatifs, déf. et caractérisation admise.
- déf. de la continuité en un point et caractérisation avec les voisinages avec démonstration.
- caractérisation globale de la continuité : une seule implication est au programme officiel: f est continue de A dans F alors la préimage d’un ouvert de F est un ouvert de A (resp. d’un fermé) : démo. non exigible, par contre : savoir bien la mettre en oeuvre pour montrer que tel ensemble est ouvert ou fermé.
- Savoir justifier qu’une application donnée est continue : théorème d’opération, continuité des formes coordonnées, et donc des fonctions polynomiales ou rationnelles.
- Définir ce qu’est un homéomorphisme et pourquoi l’image d’un ouvert par un homéo est un ouvert. Donner. un exemple de fonction continue bijective qui n’est pas un homéo.
- Sur la planche T2 : les exercices 1 à 14 sauf 7. Planche-T2-2025-2026.
- La colle commencera par un exercice de révision sur les séries numériques, assez élémentaire avec une série de terme général u_n explicite dont on détermine la nature avec les outils des développements asymptotiques et autres majorations. Pour les élèves : ce calcul ne doit pas occuper plus de 15 minutes, si possible moins (Les DL les DL les DL les DL, et potiron et O(1/n^2) nos amis).
- Montrer que la norme infinie sur l’espace des fonctions bornées sur un ensemble quelconque valeurs dans K, à est bien une norme (on sera très précis pour les arguments sur les sup.) (attention pour les étudiants le sup n’est pas supposé être un max.)
- Comparer N_1,N_2,N_infini dans R^n (inégalités).
- Montrer que N_1 et N_infini ne sont pas équivalentes dans C([0,1],R).
- Théorème pour les produits de limites de suites dans une algèbre normée (c’est à dire munie d’une norme d’algèbre, avec démonstration)
- Justifier que dans un evn de dim. finie, la convergence d’une suite se vérifie « coordonnée par coordonnée ».
- Justifier que dans un evn de dim. finie, une série absolument convergente est convergente.
- Justification de l’existence de l’exp. matricielle
- Calcul de l’exponentielle d’une matrice diagonalisable, justifier.
- Pour ce qui est de la planche T1 : tous les exercices ont été traités sauf le 9, le 11 f), le 14, le 15 c) et le 17. Planche-T1-2025-2026
- Trigonalisation : démonstration par récurrence du théorème qui dit qu’un endomorphisme ayant polynôme annulateur scindé est tz.
- Caractérisations des nilpotents en termes de v.p. dans C et autre (des équivalences très simples !)
- Théorème de décomposition sur les s.e.v. caractéristiques : il donne une tz précisée : énoncé et démonstration.
- Les élèves doivent savoir conduire la trigonalisation concrète d’une matrice 2x 2, et d’une matrice 3 x 3 donnée (exemples en cours et mieux trigonalisation sous forme de Jordan vue en exercice pour ces tailles 2×2 et 3×3)..
-
- OU BIEN une question de cours des chapitres R1,R2,R3 (trois derniers programmes de colle sem 4,5,6).
- OU BIEN un exercice d’algèbre de la banque CCINP : 59, 60, 62, 64, 65, 67 à 75 (sauf les deux systèmes différentiels au 74, 75), 83 à 91, 93, 94 (ne pas négliger les exercices sur l’arithmétique dans Z et sur les polynômes).
- banque finale sans corr session 2026
- banque finale avec corr session 2026
- OU BIEN un exercice des planches A1, A2 R1, R2, R3 :
- Planche-R3-2025-2026
- Planche-R2-2025-2026
- Planche-R1-2025-2026
- Planche-A2-2025-2026
- Planche-A1-2025-2026
- Cette semaine, tout sur la diagonalisation, les polynômes caractéristiques, Cayley-Hamilton et bien sûr tout le programme précédent. Pas de trigonalisation encore cette semaine, merci. Nous avons fait beaucoup d’exercices : tous ceux de la Planche-R2-2025-2026 ont été travaillés et corrigés en classe sauf les 7,8,9, et peuvent être reposés en colle. Penser aussi aux exercices de la banque CCINP marqués en début de planche R2 et questions suivantes :
- Calcul du polynôme caractéristique d’une matrice compagnon
- Comparaison entre le polynôme caractéristique d’un endomorphisme et celui de sa restriction à un s.e.v. stable
- Justifier que la multiplicité géométrique d’une v.p. est inférieure ou égale à sa multiplicité algébrique.
- Révisions sur les formules de changement de base, pour les vecteurs et les applications linéaires.
- valeurs propres, vecteurs propres : recherche à l’aide de l’équation aux valeurs propres sur des exemples en dim. finie ou infinie.
- caractérisation : lambda v.p. d’une matrice A ssi det(A-lambda I)=0, application aux v.p. des matrices de petites tailles et des matrices triangulaires
- Démonstration du fait que des s.e.v. propres associés à des v.p. distinctes sont en somme directe
- Si lambda est v.p. d’un endomorphisme L et si P est un polynôme alors P(lambda) est v.p. de P(L). Conséquence si P est annulateur de L, Sp(L) est inclus dans Z(P).
- Les v.p. de L sont exactement les racines du polynôme minimal de L.
- Théorème de décomposition des noyaux : démonstration pour un produit de deux polynômes. On sera spécialement attentif à la bonne compréhension des objets manipulés (P(L)(x) et pas P(L(x)) et (PQ)(L)=P(L)o Q(L) etc…)
- Savoir donner le maximum de caractérisations d’une matrice diagonalisable et la C.S. « n v.p. distinctes en dim. n » mais en fait retenir surtout et pour chaque exercice qu’il y a d’un côté le point de vue géométrique (avec les vecteurs propres et les sev propres) et de l’autre côté le point de vue algébrique (avec les polynômes annulateurs, le minimal) .
- Montrer que si f est dz, alors l’endomorphisme f_F induit par f sur un s.e.v. stable F est encore dz.
- Qu’est-ce qu’un anneau, qu’est-ce corps ? Montrer que Z/nZ est un corps ssi Z/nZ est intègre ssi n est un nombre premier.
- Plus généralement : pour a dans Z, montrer que la classe de a est inversible dans l’anneau Z/nZ ssi a et n sont premiers entre eux
- savoir définir ce qu’est un idéal et savoir la forme des idéaux de K[X] et de Z (démonstration faite dans K[X] à connaître).
- Définir le polynôme minimal d’un matrice (resp. d’un endomorphisme d’un e.v. de dim. finie) et savoir pourquoi tout polynôme annulateur est un multiple du polynôme minimal.
- Expliciter le polynôme minimal d’une matrice diagonale.
- Montrer que dim K[A]=deg(mu_A).
- Montrer que si A est une matrice inversible alors A^{-1} est dans K[A].
- Montrer que si A est une matrice et P est un polynôme alors P(A) est une matrice inversible ssi P est premier avec le polynôme minimal de A.
- Somme directe de plusieurs s.e.v.: définition par l’unicité de l’écriture, différentes caractérisation, notamment avec l’isomorphisme avec le produit direct, la caractérisation par les sommes nulles, et en dimension finie, avec les bases et la dimension.
- Matrices par blocs : produits, opérations élémentaires sur les blocs, formule du déterminant d’une matrice triangulaire par bloc (deux démonstrations faites, en donner une au choix). Les exercices consiste souvent à se ramener à cette forme triangulaire par bloc par opération ou multiplication par des matrices codant les opérations qu’on veut faire….
- Une question de révision (non faite en classe) : calcul du déterminant de Vandermonde. D’une manière générale, bien réviser le cours de 1ère année sur les déterminants : un calcul de déterminant inconnu (par bloc ou pas) sera aussi bienvenu.
- Définition de la divergence grossière, et savoir démontrer que si la série de terme général (u_n) converge alors (u_n) tend vers zéro.
- Test de d’Alembert avec démonstration.
- Citer précisément le théorème de sommation des relations de comparaison et démontrer un cas.
- Citer le Théorème sur les séries alternées spéciales avec comme conclusion aussi le signe du reste et la majoration du reste.
- Savoir mettre en oeuvre le lien suites/séries : exemple du développement asymptotique de H_n à la précision o(1/n).
- Définition de la sommabilité et de la somme d’une famille sommable : cas positif, cas signe quelconque.
- Exemple concret de manipulation de familles sommables avec le théorème de sommation par paquet : en deux temps pour le cas des familles de signe variable sur l’exemple des (-1)^p/q^p
Année 2024-2025
Semaine 23 dernière semaine, lundi 31 mars : calcul différentiel. La connaissance du cours est essentielle mais pour rassurer les élèves, on peut dire qu’ici les exercices seront de trois ou quatre types (cf. la planche, Planche-D3, faite presque entièrement sauf ex 15) – calculs de différentielles par D.L. ou autre (type ex. 5,6,7 pl) – étude du C^1 au voisinage d’un point à problème (type ex 1 à 4 pl). – étude des extrema locaux avec le calcul diff à l’ordre deux (type ex 12 à 14 pl). – pour les plus à l’aise, exercice plus théoriques utilisant souvent la dérivation le long d’une courbe (un segment) (type ex 8,9, 10,..) mais la formule de dérivation le long d’un courbe non connue donnera lieu à un zéro en colle ! Pas de vecteurs tangents, d’extrema sous contrainte ou d’E.D.P. cette semaine (et donc choisir parmi les exercices de la banque CCINP cités sur la planche ceux qui n’utilisent pas ces notions à savoir 33, 52, 56 sauf la fin (même si…), 57, 58 et pas le 41). Merci aux examinateurs de bien respecter les notations du programme sur le sujet.- Calcul différentiel d’ordre 1 :
- Définition de la dérivée D_v f(a) de la fonction f selon le vecteur v au point a et lien avec les dérivées partielles, cas où f est une norme N et a=0 ?
- Savoir qu’il existe des fonctions f telles que D_v f(a) existe pour tout v et qui ne sont pourtant pas continue en a (exemple sur la planche ou en cours).
- Définition de la différentiabilité : existence d’un D.L. 1, notation df(a).h
- définition du gradient pour les fonctions à valeurs scalaires.
- Faire BEAUCOUP de calculs de différentielle (de gradient) avec des D.L. 1 comme ceux de la planche ex 5,6,7.
- Déf. des fonctions de classe C^1 : l’application x-> df(x) est continue, mais surtout caractérisation miraculeuse avec les dérivées partielles
- Exercices concrets où l’on utilise le point précédent (cf. planche et banque CCINP).
- Formule sur la différentielle d’une composée d(f o g)=, deux cas particuliers très utiles si l’espace intermédiaire est R et surtout si l’espace de départ est R (dérivée selon une courbe à savoir par coeur !)
- Formule d’intégration le long d’un chemin. Application si df=0 sur un ouvert c.p.a. alors f est constante.
- C.N. d’extremum local en un point d’un ouvert : point critique.
- Calcul différentiel d’ordre 2 :
- fonctions C^2, C^k, théorème de Schwarz (admis)
- Calcul de la dérivée seconde de t->f(a+tx)
- Définition de la Hessienne d’une fonction f : U -> R, expliquer pourquoi c’est aussi la jacobienne du gradient de f.
- Savoir citer le théorème de Taylor-Young à l’ordre 2 (admis)
- C.N. de min. local : point critique a tel que Hf(a) soit symétrique positive (savoir dém).
- C.S. de min. local : point critique a tel que Hf(a) soit définie positive. (dém non exigée mais faite).
- Pratique en dim. 2 avec det(Hf(a)) et Tr(Hf(a)).
- Exemple où Hf(a) est dégénérée (0 v.p.) en exercice.
- Montrer le théorème de Bolzano-Weierstrass (B.W.) dans C en admettant le résultat dans R.
- Montrer qu’un compact de E est fermé borné dans E.
- Montrer qu’un fermé dans un compact est compact.
- Donner un exemple de fermé borné non compact (aussi exercice 13 banque CCINP sur ce sujet mais penser au cadre préhilbertien aussi).
- Montrer que l’image continue d’un compact est compacte.
- Théorème des bornes atteintes pour les fonctions d’un compact dans R.
- Théorème de B.W. en dimension finie (sans dém.) : deux formulations : les boules sont compactes ou les suites bornées admettent une v.a.
- Montrer qu’un s.e.v. de dim. finie est toujours fermé dans tout e.v.n.
- Parties connexes par arc (c.p.a.) de R?
- Image continue d’un c.p.a.
- Définition d’une v.a.d. : savoir vérifier les conditions de la déf. d’une v.a.d . Savoir montrer exemple que si X est une v.a.d alors pour toute fonction f, f(X) est un v.a.d.
- V.a.d. géométrique : exemple du temps d’attente du premier succès dans une suite de tirages de Bernoulli indépendante (savoir justifier ce que temps d’attente définit bien une v.a.d.)
- Loi de Poisson : déf., Convergence en loi de v.a. suivant B(n,lambda/n) vers P(lambda)
- Indépendance des v.a.d. : déf. équivalentes (dém. non demandée mais savoir faire des énoncés précis).
- Calcul d’Espérance des v.a. binomiales (2 méthodes), géométriques ou de Poisson.
- Théorème de transfert dém non exigée mais énoncé précis (deux cas). Pourquoi une v.a.d. est-elle d’espérance finie ssi E(|X|) est finie ?
- Calcul de l’espérance d’une v.a.d. à valeur dans N à l’aide des P(X>k) (dém).
- Définir ce qu’est une tribu et exemples simples sur la Planche-P1-2024-2025
- Qu’est-ce qu’une probabilité ? Démontrer la propriété de continuité croissante.
- Démontrer la sous-additivité dénombrable des probabilités (fait en exercice).
- Donner des propriétés de l’espace probabilisé décrivant le jeu à pile ou face infini (où l’existence de la proba est bien sûr admise) : quelle tribu, comment montrer que la probabilité des singletons est nulle.
- Dans l’exemple précédent donner un exemple de système quasi-complet d’événements (qui n’est pas « complet »).
- Définir ce qu’est une famille d’événements indépendants puis montrer que la formule sur la proba de l’intersection de ces événements se généralise à une famille infinie.
- Démontrer une famille pour la probabilité de l’Union de n événements A_i indépendants en fonctions des P(A_i).
- Enoncer les formules des proba composées et proba totales.
- Résolution d’un système linéaire X'(t)=A.X(t) avec A matrice constante 2×2 ou 3×3:
- Cas où A est diagonalisable dans R
- Cas où A est diagonalisable dans C et qu’on veut des solutions réelles
- Cas où A est seulement trigonalisable : on a comparé la méthode d’une simple trigonalisation ou de la réduction sous les sous-espaces caractéristiques sur des exemples. (Pour les étudiants bien revoir le chapitre R3 de réduction).
- IL serait INADMISSIBLE de ne pas savoir trigonaliser une matrice 3×3 cette semaine !! De même le calcul des vecteurs propres doit être efficace !
- Nous avons traités tous les exercices correspondants ex5 à 8 de la Planche-D2 en plus de nombreux exemples du cours. S’entraîner aussi avec ex 74, 75 de la banque CCINP.
- la méthode de variations des constantes à l’ordre deux. Là encore on pourra vérifier que la méthode est bien apprise sur des exemples concrets (calculs avec aussi révisions des calculs de primitives).
- Ne pas oublier aussi la recherche de solutions particulières développables en séries entières, la technique est importante est doit être bien travaillée.
- Une question sur le programme précédent : endomorphismes d’un espace euclidien. La planche R4-bonus-decomp-matricielles suivante aura été traitée en partie.
- Une question sur la dénombrabilité OU la dérivation des fonctions d’une variable réelle à valeurs vectorielles, comme illustré par la planche ci-jointe :Planche-P0-D1, avec comme questions de cours possibles pour la partie Dérivation
-
-
-
- Trois définitions équivalentes de la dérivabilité pour f : I -> E (dém. non demandée)
- Dérivée de L o f si f est dérivable de I dans E et L est linéaire de E dans F (dém.)
- Dérivée de B(f,g) si f (resp. g) sont dérivables de I dans E (resp. dans F) et B : E x F-> G est bilinéaire (dém.)
- Extension du point précédent aux applications n-linéaires (typiquement déterminant) (pas de dém. juste la formule)
- T.A.F. généralisé à deux fonctions » f'(c) (g(b)-g(a))=g'(c)(f(b)-f(a)) » démonstration vectorielle
- Dérivation de t-> exp(tA) par théorème de dérivation terme à terme à valeurs vectorielles (dém)
- Inégalité triangulaire pour les intégrales de fonctions vectorielles et application à l’I.A.F. dans l’hypothèse C^1.
- Formules de Taylor à savoir parfaitement.
-
-
-
-
-
-
-
- Cours: Montrer qu’une union finie ou dnb d’ensembles finis ou dnb est finie ou dnb
- Exercice (pour les motivé.e.s) : montrer que {0,1}^N (où N est l’ensemble des entiers naturels) n’est pas dénombrable à l’aide de la construction diagonale.
- Cours: Définir ce qu’on appelle le développement décimal (resp. dyadique) propre respectivement impropre d’un nombre réel dans [0,1[ (l’impropre n’existant que pour les nombres décimaux, resp. dyadiques).
-
-
-
- Définition de l’adjoint, écriture matricielle en b.o.n.
- Si F est un s.e.v. stable par u alors son orthogonal est stable par u*.
- Donner le plus de caractérisations possibles des isométries vectorielles avec dém de l’une d’elles au choix des colleurs..
- Donner le plus de caractérisations possibles des matrices orthogonales : attention déterminant =+- 1 n’est PAS une caractérisation de ces matrices !
- Montrer qu’une matrice orthogonale symétrique est une matrice de symétrie orthogonale et montrer que vous avez compris ce que chaque terme de cette phrase veut dire….
- Thme de classification de toutes les isométries vectorielles : énoncé, étapes de la preuve (sans prouver tous les lemmes utilisés, démo au choix parmi ces lemmes)
- Théorème spectral sur les endomorphismes auto adjoints : étapes de la preuve (sans prouver tous les lemmes utilisés démo au choix parmi ces lemmes).
- Pour f dans L(E), justifier que f est entièrement déterminé par sa forme bilinéaire associée (x,y)-> (x|f(y)). Si f est auto adjoint alors cette forme bilinéaire, symétrique, est entièrement connue si on connait la forme quadratique (mot H.P) q_f : x-> (x|f(x)), pourquoi ? (formule de polarisation pour q_f). Ecriture matricielle de ces objets.
- Ecriture de la forme quadratique x-> (f(x)|x) dans une b.o.n. de dz. de f auto adjoint , application à une caractérisation de la plus grande et de la plus petite v.p. de f.
- Définition des autoadjoints positifs (resp. matrices symétriques positives) et caractérisation par le spectre.
- Définir le produit scalaire canonique de R^n, dans M_{m,n}(R) (deux expressions montrer qu’elles coïncident)
- Produit scalaire dans l^2(N,R) (justifier la convergence de la série…)
- Produit scalaire dans L^2,continue(I,R) (justifier la convergence des l’intégrale)
- (Les justifications des exemples précédents n’ont pas tous été détaillés en classe ou bien fait dans d’autres chapitres (I1 pour L^2(I,R), ne pas hésiter à me demander en cas de pb).
- Expliquer pourquoi le p.s. est une application bilinéaire CONTINUE (savoir la caractérisation des appli. bilinéaires continues).
- Montrer que l’orthogonal d’une partie dense est réduit à {0}. Application au ‘lemme des moments’ (Banque CCINP 48 même si le corrigé de la banque est formulé sans produit scalaire, voir la rédaction faite en classe !).
- Lemme de représentation de Riesz pour les formes linéaires d’un espace euclidien.
- Montrer que l’orthogonal d’une partie A de E est un s.e.v. fermé de E.
- Existence d’un supplémentaire orthogonal pour un s.e.v. de dim. finie d’un espace préhilbertien.
- Formule de calcul de la projection orthogonale quand on connait une base orthogonale de ce s.e.v. : applications sur des exemples, cas des sommes partielles de la série de Fourier de f.
- Le projeté orthogonal d’un vecteur v sur un sev F est l’unique vecteur de F qui minimise la distance entre v et les vecteurs de F.
- Mise en oeuvre de l’orthogonalisation de Gram-Schmidt sur des exemples.
- exercices 1 à 30 sauf l’ex 13,
- exercices 43 à 54 sauf l’ex 48 et l’ex. 52
- version à variable continue du théorème de convergence dominée,
- théorème de continuité pour les intégrales à paramètres
- théorème sur le caractère C^k des intégrales à paramètres
- Continuité de la TF (transformée de Fourier) d’une fonction intégrable
- Continuité sur ]0,+oo[ de la TL (transformée de Laplace) d’une fonction c.p.m. bornée, extension à la variable complexe.
- Théorème de la valeur initiale pour la transformée de Laplace dans le cas facile d’une fonction bornée : L(f)(x)=f(0)/x+ o(1/x) quand x–>+oo.
- Lemme de Riemann-Lebesgue dans le cas facile où f est de classe C^1 et f et f’ sont intégrables : F(f)(x) –>0 pour x–>+oo
- Caractère C^1 et dérivation de la TL du sinus cardinal sur l’ouvert ]0,+oo[ : application au calcul de cette Transformée.
- Calcul de la dérivée p-ième de la TF d’une fonction f telle que pour tout k=0,1,..p, la fonction t-> t^k f(t) doit intégrable. (Si ceci est vrai pour tout p, on dit que la fonction est « à décroissance rapide »).
- Etude complète de la fonction Gamma : notamment justification soigneuse du caractère C^k et justifications pour le tracé du graphe.
- REVOIR les techniques de calculs d’intégrales et de primitives (1ère année, planche I1).
- Bien savoir aussi dériver si x est dans les bornes des intégrales (1ère année… et pas que..)
- Lemme d’Abel, dém. et (prop.-)-définition du rayon de convergence.
- Test de d’Alembert pour les séries entières : dém. avec le lemme pour les séries numériques laissée en exercice en cours, mais faite sur les exemples des séries lacunaires ensuite en exercices !
- Prop. :
 ont même rayon de convergence (au programme officiel pour alpha=1, démontrée, pour pas plus cher pour alpha qcq donc je pense qu’on peut s’en servir pour alpha quelconque).
ont même rayon de convergence (au programme officiel pour alpha=1, démontrée, pour pas plus cher pour alpha qcq donc je pense qu’on peut s’en servir pour alpha quelconque). - Rayon de convergence d’une somme et produit de Cauchy.
- Continuité de la fonction somme dans le disque ouvert de convergence.
- Pour ce qui la variable est réelle :
- Théorème de continuité radiale d’Abel : énoncé seulement, mais savoir l’appliquer sur des exemples (série harmonique alternée…)
- Dérivation terme à terme automatique pour les sommes de séries entières
- unicité des coefficients du D.S.E., série de Taylor, rigidité des fonctions D.S.E.
- DSE des fonctions usuelles : preuve de la formule du binôme (1+x)^a pour a réel avec la méthode de l’E.D. ou avec une formule de Taylor au moins pour x>0.
- Banque CCINP cf haut de la planche. Planche-S3-2024-2025 Nous avons traités les exercices 1 à 9 et 11, 12, nous traiterons au moins jusqu’au 14.
- Citer très précisément les deux théorèmes d’intégration d’une limite (celui avec la CVU sur un segment vs le T.C.D. de Lebesgue) : lesquels sait-on démontrer 🙂 ?
- Donner un exemple d’une suite de fonctions (f_n) qui Converge Uniformément sur un intervalle I (non borné) vers une fonction f et telle que l’intégrale sur I des f_n ne converge PAS vers l’intégrale sur I de f (étalement de la bosse : un dessin peut suffire, une fois transformé en fonction affine par morceau).
- Application du T.C.D. avec des « bornes variables » exemple de la limite de
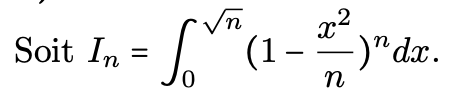
- Etude des intégrales de Wallis : détermination d’un équivalent. Toutes les étapes (relation de récurrence, invariant, encadrement) doivent être mémorisées.
- Méthode l’I.P.P fait sortir le terme prépondérant pour un équivalent, si f(1) non nul, de :
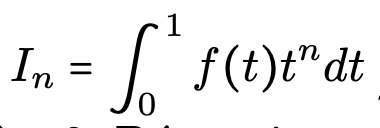
- Méthode l’I.P.P fait sortir le terme prépondérant pour un équivalent, si f(1) non nul, de :
- Le même équivalent par la méthode de changement de variable.
- Intégration terme à terme d’une CVU sur un segment :
-
- application aux séries entières, comment obtenir le D.S.E. de ln(1+x) à partir de celui de 1/(1+x)
sur ]-1,1[.
- application à la formule donnant les coefficients a_n et b_n d’une série trigonométrique comme des intégrales sur sa somme (formule des coeff. de Fourier).
- application aux séries entières, comment obtenir le D.S.E. de ln(1+x) à partir de celui de 1/(1+x)
-
- Théorème d’intégration terme à terme de Lebesgue en deux théorèmes : cas positif et cas signe quelconque. Donner des énoncés précis !
- Ce qu’on fait quand le théorème ne s’applique pas (notamment en cas de Cv par théorème des séries alternées spéciales).
- Planche I2 : tous les exercices de la planche auront été traités. Planche-I2-2024-2025
- Banque CCINP : pour réviser les séries de fonctions, ex. 14.1,14.2,15, 16,17.
- On pourra demander un énoncé précis de théorème en début de colle.
- Démonstration du théorème de continuité d’une limite uniforme d’une suite de fonction continue.
- Démonstration du théorème d’intégration d’une limite uniforme sur un segment.
- Le théorème d’interversion des limites a été admis.
- Exemple de la fonction zeta réelle : caractère C infini, limite à l’infini
- Exemple de la suite de fonctions x-> n sin(x/n) méthode pour la CVU sur les segments et pourquoi on n’ a pas CVU sur R
- Méthode d’encadrement par des intégrales pour un équivalent quand x->1 de la fonction zeta
- ouverts et fermés relatifs : définition d’un ouvert de A, d’un fermé de A, caractérisations (démo non exigibles mais énoncés à bien connaître).
- v
- Montrer que la norme infinie sur l’espace des fonctions bornées est bien une norme (on sera très précis pour les arguments sur les sup.)
- Comparer N_1,N_2,N_infini dans R^n (inégalités).
- Montrer que N_1 et N_infini ne sont pas équivalentes dans C([0,1],R).
- définir ce qu’est une norme d’algèbre, en donner des exemples dans l’algèbre des fonctions bornées, et dans l’algèbre des matrices carrées.
- Théorème pour les produits de limites de suites dans une algèbre normée (avec démonstration)
- Justifier que dans un evn de dim. finie, la convergence d’une suite se vérifie « coordonnée par coordonnée ».
- Justifier que dans un evn de dim. finie, une série absolument convergente est convergente.
- Justification de l’existence de l’exp. matricielle.
- Montrer qu’une boule ouverte est ouverte, qu’une boule fermée est fermée
- Montrer que l’intérieur d’une boule fermée est la boule ouverte
- Montrer que l’adhérence d’une boule ouverte est la boule fermée
- Exercice : Montrer qu’un s.e.v. strict est d’intérieur vide.
- Caractérisation séquentielle des points adhérents.
- Lien complémentaire de l’adhérence/intérieur du complémentaire..
- Trigonalisation : démonstration par récurrence du théorème qui dit qu’un endomorphisme ayant polynôme annulateur scindé est tz.
- Caractérisations des nilpotents en termes de v.p. dans C et autre (des équivalences très simples !)
- Les élèves doivent savoir conduire la trigonalisation concrète d’une matrice 2x 2, et d’une matrice 3 x 3 donnée et même la réduction sous forme de Jordan sur ces exemples 2×2 et 3×3.
- Théorème de décomposition sur les s.e.v. caractéristiques : il donne une tz précisée : énoncé et démonstration.
- Un exercice d’algèbre de la banque CCINP : 59, 60, 61 sauf 3), 62, 64, 65, 67 à 75 (sauf les deux systèmes différentiels au 74, 75), 83 à 91, 93, 94 (ne pas négliger les exercices sur l’arithmétique dans Z et sur les polynômes)
- Une question de réduction qui peut encore être une QdC ou un exercice des planches R1, R2, R3 ou quelque chose de proche mais aussi bien un exercice inconnu.
- Planche-R3-2024-2025Planche-R2-2024-2025Planche-R1-2024-2025
- Cette semaine, tout sur la diagonalisation, les polynômes caractéristiques, Cayley-Hamilton et bien sûr tout le programme précédents. Pas de trigonalisation encore cette semaine, merci. Nous avons fait beaucoup d’exercices : tous ceux de la Planche-R2 ont été travaillés et corrigés en classe sauf l’ex 13 et 14 et peuvent être reposés en colle. Penser aussi aux exercices de la banque CCINP marqués en début de planche R2 et questions suivantes :
- Calcul du polynôme caractéristique d’une matrice compagnon
- Justifier que la multiplicité géométrique d’une v.p. est inférieure ou égale à sa multiplicité algébrique.
- Démonstration de Cayley Hamilton dans le cas particulier compagnon avec le calcul du polynôme minimal.
- Révisions sur les formules de changement de base, pour les vecteurs et les applications linéaires.
- valeurs propres, vecteurs propres : recherche à l’aide de l’équation aux valeurs propres sur des exemples en dim. finie ou infinie.
- caractérisation : lambda v.p. d’une matrice A ssi det(A-lambda I)=0, application aux v.p. des matrices de petites tailles et des matrices triangulaires
- Démonstration du fait que des s.e.v. propres associés à des v.p. distinctes sont en somme directe
- Si lambda est v.p. d’un endomorphisme L et si P est un polynôme alors P(lambda) est v.p. de P(L). Conséquence si P est annulateur de L, Sp(L) est inclus dans Z(P).
- Les v.p. de L sont exactement les racines du polynôme minimal de L.
- Théorème de décomposition des noyaux : démonstration pour un produit de deux polynômes. On sera spécialement attentif à la bonne compréhension des objets manipulés (P(L)(x) et pas P(L(x)) et (PQ)(L)=P(L)o Q(L) etc…)
- Savoir donner le maximum de caractérisations d’une matrice diagonalisable et la C.S. « n v.p. distinctes en dim. n » mais en fait retenir surtout et pour chaque exercice qu’il y a d’un côté le point de vue géométrique (avec les vecteurs propres et les sev propres) et de l’autre côté le point de vue algébrique (avec les polynômes annulateurs, le minimal) .
- Montrer que si f est dz, alors l’endomorphisme f_F induit par f sur un s.e.v. stable F est encore dz.
- Qu’est-ce qu’un anneau, qu’est-ce corps ? Montrer que Z/nZ est un corps ssi Z/nZ est intègre ssi n est un nombre premier.
- Plus généralement : pour a dans Z, montrer que la classe de a est inversible dans l’anneau Z/nZ ssi a et n sont premiers entre eux
- savoir définir ce qu’est un idéal et savoir la forme des idéaux de K[X] et de Z (démonstration faite dans K[X]).
- Définir le polynôme minimal d’un matrice (resp. d’un endomorphisme d’un e.v. de dim. finie) et savoir pourquoi tout polynôme annulateur est un multiple du polynôme minimal.
- Expliciter le polynôme minimal d’une matrice diagonale.
- Montrer que dim K[A]=deg(mu_A).
- Montrer que si A est une matrice inversible alors A^{-1} est dans K[A].
- Montrer que si A est une matrice et P est un polynôme alors P(A) est une matrice inversible ssi P est premier avec le polynôme minimal de A.
- Somme directe de plusieurs s.e.v.: définitions, différentes caractérisations
- Matrices par blocs : produits, opérations élémentaires sur les blocs, formule du déterminant d’une matrice triangulaire par bloc (deux démonstrations).
- Question de cours :
- citer le plus de caractérisations possibles de « F est somme directe de F_1+..+F_m »
- valeur et calcul du déterminant de Vandermonde
- définition de la comatrice et « formule de la comatrice » (sans dém)
- théorème caractérisant le rang d’une matrice avec les matrices extraites inversibles (sans dém)
- Définition de la divergence grossière : savoir démontrer que si la série de terme général (u_n) converge alors (u_n) tend vers zéro.
- Test de d’Alembert avec démonstration.
- Citer précisément le théorème de sommation des relations de comparaison et démontrer qu’il entraîne le théorème de convergence en moyenne de Cesaro.
- Savoir justifier le développement asymptotique de H_n à la précision o(1) de deux façons différentes (il y en a trois dans le cours).
- On peut aussi demander le terme d’après du développement asymptotique de H_n.
- Pour les familles sommables : citer les deux théorèmes de sommation par paquets (cas positifs, cas quelconque) et savoir s’en servir pour la sommation des (-1)^p/q^p.
- Résolution d’un système linéaire X'(t)=A.X(t) avec A matrice constante 2×2 ou 3×3:
- Cas où A est diagonalisable dans R
- Cas où A est diagonalisable dans C et qu’on veut des solutions réelles
- Cas où A est seulement trigonalisable : on a comparé la méthode d’une simple trigonalisation ou de la réduction sous les sous-espaces caractéristique sur des exemples. (Pour les étudiants bien revoir le chapitre R3 de réduction).
- Résolution d’équations différentielles linéaires scalaires d’ordre deux :
- Méthodes de première année : MVC à l’ordre 1, calculs des primitives, recollement des solutions des E.D. singulières( premier ordre ex 1,2 pl. D3 et un exercice sur la banque CCINP), cas des second membres particuliers des équations à coeff. constant (cf. ex. 6,7 pl. D3)
- Méthode de la variation Des constantes pour les ED d’ordre deux : à bien maîtriser.
- Quand on ne connaît pas de solutions de l’équation homogène : exemple de recherche des solutions D.S.E. (pratique à bien maîtriser !)
- Quand on connaît une solution de l’équation homogène et qu’on en vu une autre indépendante, technique de la réduction de l’ordre par variation de la constante (ou via le Wronskien)
- Pour les équations aux dérivées partielles : technique du changement de variable (et de fonctions) : cette technique s’applique aussi aux équations différentielles ordinaires du reste mais dans tous les cas, les changements de variables doivent être donnés.
-
- Vecteur tangent en un point x à un sous-ensemble X de R^n : définition, exemples, structure de cône de l’ensemble T_x X de ces vecteurs.
- Exemple si X est une sphère (savoir refaire) dans R^n.
- Cas général si x est un point régulier d’une hypersurface X définie par l’équation g=0 alors T_x X est l’hyperplan défini par ker dg(x) (une inclusion admise dans le cadre général : dans certains exemples, on montre l’inclusion manquante)
- C.N. d’extremum pour f en un point x d’un ouvert U : df(x)=0 (point critique).
- C.N. d’extremum pour f_|X où X sous ensemble qcq : T_x X inclus dans Ker df(x)
- C.N. d’extremum pour f_|X en un point régulier x d’une hypersurface d’équation g=0 : df(x)= k dg(x).
- Calcul différentiel d’ordre 2 :
- fonctions C^2, C^k, théorème de Schwarz (admis)
- Calcul (important) de la dérivée seconde de t->f(a+tx)
- Définition de la Hessienne d’une fonction f : U -> R, c’est aussi la jacobienne du gradient de f.
- Savoir citer le théorème de Taylor-Young à l’ordre 2 (admis)
- C.N. de min. local : point critique a tel que Hf(a) soit symétrique positive (savoir dém).
- C.S. de min. local : point critique a tel que Hf(a) soit définie positive. (savoir dém.)
- Pratique en dim. 2 avec det(Hf(a)) et Tr(Hf(a)).
- Exemple où Hf(a) est dégénérée (0 v.p.) en exercice.
- Calcul différentiel d’ordre 2 :
- Trois définitions équivalentes de la dérivabilité pour f : I -> E (dém. non demandée)
- Dérivée de L o f si f est dérivable de I dans E et L est linéaire de E dans F (dém.) : à reméditer après le cours de calcul diff.
- Dérivée de B(f,g) si f (resp. g) sont dérivables de I dans E (resp. dans F) et B : E x F-> G est bilinéaire.
- Extension du point précédent aux applications n-linéaires (typiquement déterminant).
- Dérivation de t-> exp(tA) par théorème de dérivation terme à terme à valeurs vectorielles.
- Inégalité triangulaire pour les intégrales de fonctions vectorielles et application à l’I.A.F. dans l’hypothèse C^1.
- Formules de Taylor à savoir parfaitement (ne pas hésiter à le vérifier …)
-
- Définition de la dérivée D_v f(a) de la fonction f selon le vecteur v au point a et lien avec les dérivées partielles, cas où f est une norme N et a=0 ?
- Savoir qu’il existe des fonctions f telles que D_v f(a) existe pour tout v et qui ne sont pourtant pas continues en a (exemple donné en cours pas à savoir par coeur).
- Définition de la différentiabilité notation df(x).h, existence d’un D.L. 1, et définition du gradient pour les fonctions à valeurs réelles . La différentiabilité entraîne la continuité et l’existence des dérivées suivant tout vecteur.
- Exemples concrets de calculs de DL 1 et notamment dans le cadre matriciel cf. ex. 4, (crucial !) et ex 5 planche et exo de cours sur M-> M^{-1}.
- Déf. de f C^1 et caractérisation cruciale (admise) avec la continuité des dérivées partielles à utiliser sur des exemples.
- Différentielle d’un produit et d’une fonction composée et notamment la formule de dérivation le long d’une courbe.
- Tous les exercices des deux planches ont été faits sauf le dernier de chaque planche. Planche-D1-2023Planche-D2-2023
- Moments d’ordre r d’une v.a.d. : si X admet un moment d’ordre r alors X admet un moment d’ordre s pour tout s<r.
- Calculs des variances des lois usuelles et notamment géométriques et Poisson et cas de loi binomiale comme sommes de v.a. indépendantes
- Covariance : déf., application à la variance d’une somme
- Deux inégalités de Cauchy-Schwarz dans le contexte probabiliste, l’une avec (X,Y)->E(XY), l’autre avec la covariance,
- fonction génératrice : deux définitions. La série génératrice détermine la loi.
- Fonction génératrice d’une somme de v.a.d. indépendantes application à la loi binomiale, à la somme de deux v.a. de Poisson indépendantes
- Calcul de l’espérance en dérivant la fonction génératrice (justifier).
- Inégalité de Markov et de Tchebychev.
- Loi faible des grands nombres: énoncé et démonstration.
- Définition d’une v.a.d. : savoir vérifier les conditions de la déf. d’une v.a.d : exemple du temps d’attente de succès dans une suite de tirages de Bernoulli (v.a.d. de loi géométrique) ou de l’exercice 1 de la planche P2.
- Caractérisation des v.a. géométriques par le caractère « sans-mémoire ».
- Convergence en loi de v.a. suivant B(n,lambda/n) vers P(lambda)
- Indépendance des v.a.d. : déf. équivalentes (dém. non demandée mais savoir faire des énoncés précis).
- Espérance des v.a. géométriques ou de Poisson.
- Théorème de transfert dém non exigée mais énoncé précis (deux cas). Pourquoi une v.a.d. est-elle d’espérance finie ssi E(|X|) est finie ?
- Calcul de l’espérance d’une v.a.d. à valeur dans N à l’aide des P(X>k) (dém).
- une question d’algèbre linéaire ou d’algèbre commutative qui peut être :
- un exercice de la banque CCINP partie algèbre tout (ex. 59 à 93) : on laissera juste de côté les exercices 74,75.
- un exercice d’une des planches (ou variante simple de ceux-ci) d’algèbre de cette année : les revoici par commodité ici
- Définition de l’adjoint, écriture matricielle en b.o.n.
- Si F est un s.e.v. stable par u alors son orthogonal est stable par u*.
- Donner le plus de caractérisations possibles des isométries vectorielles avec dém de l’une d’elles
- Donner le plus de caractérisations possibles des matrices orthogonales : attention déterminant =+- 1 n’est PAS une caractérisation de ces matrices !
- Montrer qu’une matrice orthogonale symétrique est une matrice de symétrie orthogonale et montrer que vous avez compris ce que chaque terme de cette phrase veut dire….
- Thme de classification de toutes les isométries vectorielles : énoncé, étapes de la preuve (sans prouver les lemmes utilisés), le colleur peut demander de rédiger formellement la récurrence ce que nous n’avons pas fait en cours : dans ce cas cf. rédaction de l’ex. 2 pl. R4.
- Théorème spectral de réduction des endomorphismes auto adjoints : étapes de la preuve (sans prouver les lemmes utilisés).
- Pour f dans L(E), justifier que f est entièrement déterminé par sa forme bilinéaire associée (x,y)-> (x|f(y)). Si f est auto adjoint alors cette forme bilinéaire, symétrique, est entièrement connue si on connait la forme quadratique (mot H.P) q_f : x-> (x|f(x)), pourquoi ? (formule de polarisation pour q_f). Ecriture matricielle de ces objets.
- Ecriture de la forme quadratique x-> (f(x)|x) dans une b.o.n. de dz. de f auto adjoint , application à une caractérisation de la plus grande et de la plus petite v.p. de f.
- Définition des autoadjoints positifs (resp. matrices symétriques positives) et caractérisation par le spectre.
- Citer le théorème d’approximation uniforme des fonctions c.p.m. par des fonctions en escalier et savoir l’appliquer pour démontrer le théorème de Riemann-Lebesgue sur un segment (thme H.P. mais à connaître aussi bien pour le résultat que pour la méthode).
- Citer le théorème d’approximation de Weierstrass et montrer qu’on ne peut pas espérer une CVU sur R entier car si une suite de polynômes CVU sur R entier….
- Dans le cadre préhilbertien : montrer que l’orthogonal d’une partie dense est réduit à {0}. Application au ‘lemme des moments’ (Banque CCINP 48 même si le corrigé de la banque est formulé sans produit scalaire, voir la rédaction faite en classe !).
- Montrer que L^2_continue(I,R) est un espace préhilbertien.
- Déterminer l’orthogonal des suites nulles A.P.C.R. dans l^2(N).
- Révision de première année : CNS d’égalité dans l’inégalité de Cauchy-Schwarz et dans l’inégalité triangulaire.
- Existence d’un supplémentaire orthogonal pour un s.e.v. de dim. finie d’un espace préhilbertien.
- Formule de calcul de la projection orthogonale quand on connait une base orthogonale de ce s.e.v. : applications sur des exemples, cas des sommes partielles de la série de Fourier de f.
- Le projeté orthogonal d’un vecteur v sur un sev F minimise la distance entre v et les vecteurs de F.
- Mise en oeuvre de l’orthogonalisation de Gram- Schmidt sur des exemples.
- Montrer le théorème de Bolzano-Weierstrass (B.W.) dans C en admettant le résultat dans R.
- Montrer qu’un compact d’un e.v.n. E est fermé borné dans E.
- Montrer qu’un fermé dans un compact est compact.
- Donner un exemple de fermé borné non compact (aussi exercice 13 banque CCINP sur ce sujet mais on peut aussi penser au cadre préhilbertien avec une famille o.n.).
- Montrer que l’image continue d’un compact est compacte.
- Théorème des bornes atteintes pour les fonctions d’un compact dans R.
- Montrer que la sphère unité d’un e.v.n. de dim au moins 2 est connexe par arcs.
- L’image continue d’un c.p.a. est c.p.a.
- Connexité par arc pour montrer qu’une fonction d’un intervalle I de R dans R continue injective est strictement monotone.
- Un exercice de la Banque CCINP : Exercices 1 à 12, 14 à 32, 46, 47, 49 à 51 et 53.
- Un exercice » inconnu » (ou pourquoi pas un exercice d’une planche pour vérifier aussi que ces exercices ont été assimilés !) Par commodité je reposte ici ces planches : Planche-I3-2023Planche-S3-2023Planche-I2-2023Planche-S2-2023Planche-I1-2023Planche-S1-2023
- version à variable continue du théorème de convergence dominée,
- théorème de continuité pour les intégrales à paramètres
- théorème sur le caractère C^k des intégrales à paramètres
- Continuité de la TF (transformée de Fourier) d’une fonction intégrable
- Continuité sur ]0,+oo[ de la TL (transformée de Laplace) d’une fonction c.p.m. bornée, extension à la variable complexe.
- Théorème de la valeur initiale pour la transformée de Laplace dans le cas facile d’une fonction bornée : L(f)(x)=f(0)/x+ o(1/x) quand x–>+oo.
- Lemme de Riemann-Lebesgue dans le cas facile où f est de classe C^1 et f et f’ sont intégrables : F(f)(x) –>0 pour x–>+oo
- Caractère C^1 et dérivation de la TL du sinus cardinal sur l’ouvert ]0,+oo[ : application au calcul de cette Transformée.
- Calcul de la dérivée p-ième de la TF d’une fonction f telle que pour tout k=0,1,..p, la fonction t-> t^k f(t) doit intégrable. (Si ceci est vrai pour tout p, on dit que la fonction est « à décroissance rapide »).
- Etude complète de la fonction Gamma : notamment justification soigneuse du caractère C^k et justifications pour le tracé du graphe.
- REVOIR les techniques de calculs d’intégrales et de primitives (1ère année, planche I1).
- Bien savoir aussi dériver si x est dans les bornes des intégrales (1ère année… et pas que..)
- Lemme d’Abel, dém. et (prop.-)-définition du rayon de convergence.
- Lemme de d’Alembert pour les séries entières : dém. avec le lemme pour les séries numériques.
- Prop. ;
 ont même rayon de convergence (au programme officiel pour alpha=1, démontrée, pour pas plus cher pour alpha qcq donc je pense qu’on peut s’en servir pour alpha quelconque).
ont même rayon de convergence (au programme officiel pour alpha=1, démontrée, pour pas plus cher pour alpha qcq donc je pense qu’on peut s’en servir pour alpha quelconque). - Rayon de convergence d’une somme et produit de Cauchy.
- Continuité de la fonction somme dans le disque ouvert de convergence.
- Pour ce qui la variable est réelle :
- Théorème de continuité radiale d’Abel : énoncé seulement, mais savoir l’appliquer sur des exemples (série harmonique alternée…)
- Dérivation terme à terme automatique pour les sommes de séries entières
- unicité des coefficients du D.S.E., série de Taylor, rigidité des fonctions D.S.E.
- DSE des fonctions usuelles : preuve de la formule du binôme (1+x)^a pour a réel avec la méthode de l’E.D. ou avec une formule de Taylor au moins pour x>0.
- Banque CCINP cf haut de la planche. Planche-S3-2023
- Citer très précisément les deux théorèmes d’intégration d’une limite (celui avec la CVU sur un segment vs le T.C.D. de Lebesgue) : lesquels sait-on démontrer 🙂 ?
- Donner un exemple d’une suite de fonctions (f_n) qui CVU sur un intervalle I (non borné) vers une fonction f et telle que l’intégrale sur I des f_n ne converge PAS vers l’intégrale sur I de f.
- Application du T.C.D. avec des « bornes variables »
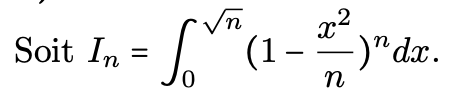
- Etude des intégrales de Wallis : détermination d’un équivalent. Toutes les étapes (relation de récurrence, invariant, encadrement) doivent être mémorisées.
- Méthode l’I.P.P fait sortir le terme prépondérant pour un équivalent de :
- Le même équivalent par la méthode de changement de variable.
- Intégration terme à terme d’une CVU sur un segment :
-
- application aux séries entières : (on admet la CvN sur les segments inclus dans ]-R,R[) montrer que :
- applications aux séries trigonométriques (très important car H.P. mais dans tellement de sujets d’écrits de maths et dans le cours de physique)
- application aux séries entières : (on admet la CvN sur les segments inclus dans ]-R,R[) montrer que :
-
- Théorème d’intégration terme à terme de Lebesgue en deux théorèmes : cas positif et cas signe quelconque. Donner des énoncés précis !
- Exemple du second cas :
- Ce qu’on fait quand le théorème ne s’applique pas. Exemple :
- Planche I2 : les exercices 1 à 5 ont été déjà faits en classe. Planche-I2-2023
- On pourra demander un énoncé précis de théorème en début de colle.
- Démonstration du théorème de continuité d’une limite uniforme d’une suite de fonction continue.
- Démonstration du théorème d’intégration d’une limite uniforme sur un segment.
- Le théorème d’interversion des limites a été admis.
- Exemple de la fonction zeta réelle : caractère C infini, variations, convexité, limite à l’infini
- Pour les plus à l’aise : limite de zeta en 1.
- Exemple de la suite de fonctions x-> n sin(x/n) méthode pour la CVU sur les segments et pourquoi on n’ a pas CVU sur R
- Méthode d’encadrement par des intégrales pour un équivalent quand x->0 de la somme des exp(-x sqrt(n)).
- ouverts et fermés relatifs : définition d’un ouvert de A, d’un fermé de A, caractérisations (démo non exigibles).
- déf. de la continuité en un point et caractérisation avec les voisinages avec démonstration.
- caractérisation globale de la continuité : f est continue de A dans F ssi la préimage d’un ouvert de F est un ouvert de A (resp. d’un fermé) : démo. non exigible, par contre : savoir bien la mettre en oeuvre pour montrer que tel ensemble est ouvert ou fermé.
- Savoir justifier qu’une application donnée est continue : théorème d’opération, continuité des formes coordonnées, et donc des fonctions polynomiales ou rationnelles.
- Savoir étudier la continuité d’une fonction en un point à problème (ex. 6,7 pl. T2).
- Exercice : Justifier la continuité de l’application A -> A^{-1} de GL_n(K) dans lui-même.
- Définir ce qu’est un homéomorphisme et pourquoi l’image d’un ouvert par un homéo est un ouvert. Donner. un exemple de fonction continue bijective qui n’est pas un homéo.
- Caractérisation de la continuité des applications linéaires : 5 conditions, avec dém.
- Définition de la norme d’opérateur (trois formules équivalentes) avec dém.
- Calcul pratique de normes d’opérateur sur des exemples : seulement à partir de mercredi !
- Montrer que la norme infinie sur l’espace des fonctions bornées est bien une norme (on sera très précis pour les arguments sur les sup.)
- définir ce qu’est une norme d’algèbre, en donner des exemples dans l’algèbre des fonctions bornées, et dans l’algèbre des matrices carrées.
- Théorème pour les produits de limites de suites dans une algèbre normée.
- Justifier que dans un evn de dim. finie, la convergence d’une suite se vérifie « coordonnée par coordonnée ».
- Justifier que dans un evn de dim. finie, une série absolument convergente est convergente.
- Justification de l’existence de l’exp. matricielle.
- Montrer qu’une boule ouverte est ouverte.
- Montrer que l’intérieur d’une boule fermée est la boule ouverte
- Montrer que l’adhérence d’une boule ouverte est la boule fermée
- Exercice : Montrer qu’un s.e.v. strict est d’intérieur vide.
- Caractérisation séquentielle des points adhérents.
- Lien complémentaire de l’adhérence/intérieur du complémentaire..
- Trigonalisation : démonstration par récurrence du théorème qui dit qu’un endomorphisme ayant polynôme annulateur scindé est tz.
- Caractérisations des nilpotents en termes de v.p. dans C et autre (des équivalences très simples !)
- Les élèves doivent savoir conduire la trigonalisation concrète d’une matrice 2x 2, et d’une matrice 3 x 3 donnée et même la réduction sous forme de Jordan sur ces exemples 2×2 et 3×3.
- Théorème de décomposition sur les s.e.v. caractéristiques : il donne une tz précisée.
- Justifier que la multiplicité géométrique d’une v.p. est inférieure ou égale à sa multiplicité algébrique.
- Démonstration de Cayley Hamilton dans le cas particulier d’une matrice dz.
- Révisions sur les formules de changement de base, pour les vecteurs et les applications linéaires.
- valeurs propres, vecteurs propres : recherche à l’aide de l’équation aux valeurs propres sur des exemples en dim. finie ou infinie
- caractérisation : lambda v.p. d’une matrice A ssi det(A-lambda I)=0, application aux v.p. des matrices de petites tailles et des matrices triangulaires
- Démonstration du fait que des s.e.v. propres associés à des v.p. distinctes sont en somme directe
- Si lambda est v.p. d’un endomorphisme L et si P est un polynôme alors P(lambda) est v.p. de P(L). Conséquence si P est annulateur de L, Sp(L) est inclus dans Z(P).
- Les v.p. de L sont exactement les racines du polynôme minimal de L.
- Théorème de décomposition des noyaux : démonstration pour un produit de deux polynômes. On sera spécialement attentif à la bonne compréhension des objets manipulés (P(L)(x) et pas P(L(x)) et (PQ)(L)=P(L)o Q(L) etc…)
- Savoir donner le maximum de caractérisations d’une matrice diagonalisable et la C.S. « n v.p. distinctes en dim. n » mais en fait retenir surtout et pour chaque exercice qu’il y a d »un côté le point de vue géométrique (avec les vecteurs propres et les ses propres) et le point de vue algébrique (avec les polynômes annulateurs, le minimal;
- Qu’est-ce qu’un anneau, qu’est-ce corps ? Montrer que Z/nZ est un corps ssi Z/nZ est intègre ssi n est un nombre premier.
- Plus généralement : pour a dans Z, montrer que la classe de a est inversible dans l’anneau Z/nZ ssi a et n sont premiers entre eux
- savoir définir ce qu’est un idéal et savoir la forme des idéaux de K[X] et de Z (dém. sur K[X]).
- Définir le polynôme minimal d’un matrice (resp. d’un endomorphisme d’un e.v. de dim. finie) et savoir pourquoi tout polynôme annulateur est divisible par le polynôme minimal.
- Expliciter le polynôme minimal d’une matrice diagonale.
- Montrer que dim K[A]=deg(mu_A).
- Montrer que si A est une matrice inversible alors A^{-1} est dans K[A].
- Montrer que si A est une matrice et P est un polynôme alors P(A) est une matrice inversible ssi P est premier avec le polynôme minimal de A.
- Somme directe de plusieurs s.e.v.: définitions, différentes caractérisations
- Matrices par blocs : produits, opérations élémentaires sur les blocs, formule du déterminant d’une matrice triangulaire par bloc (deux démonstrations).
- Définition de la divergence grossière, et savoir démontrer que si la série de terme général (u_n) converge alors (u_n) tend vers zéro.
- Test de d’Alembert avec démonstration.
- Sur la comparaison série/intégrale, pour les colleurs le programme officiel a un peu changé il s’agit maintenant plus d’un savoir faire que d’un résultat, savoir justifier le D.A. de H_n à la précision o(1).
- Citer précisément le théorème de sommation des relations de comparaison et démontrer un cas.
- Citer le Théorème spécial pour certaines séries alternées avec comme conclusion aussi le signe du reste et la majoration du reste.
- Savoir mettre en oeuvre le lien suites/séries pour gagner un terme supplémentaire dans le D.A. de H_n. (précision o(1/n)) ou donner l’idée de la preuve de la formule de Stirling et en faire une ou deux étapes.
- Révisions sur les suites récurrentes u_{n+1}=f(u_n) ou les suites définies
- Familles sommables : savoir bien distinguer entre le cas positifs et le cas à signe variable/complexe. Savoir bien mettre en oeuvre le théorème de sommation terme par paquets sans justification particulière que la positivité dans le cas positif, et au contraire avec justification préalable de la sommabilité dans le cas général.. justement avec le T.S.P. positif.
Banque CCINP ex 1 à 20 et 59 à 76. (Ne tardez pas à réviser ces exercices CCINP vous devez les connaître sur les bouts des doigts).
Pour la semaine du 30 mai au 2 juin : ex 1 à 25 et 50 à 83.
Pour la semaine du 5 juin au 10 juin : ex 1 à 45 et 50 à 94.
A partir du 12 juin : toute la banque.
Semaine 23 : du lundi 27 mars
Attention : dernière semaine de colles avant les écrits.
Thème : calcul différentiel, révision du programme précédent et les rajouts qui suivent. Par ailleurs, on peut aussi poser des questions de révisions sur les endomorphismes d’un espace euclidien.
Calcul diff. on rajoute :
-
- Exemple de recherches d’extrema sous-contrainte i.e. pour f_X
- théorème dans le cas où X est une hypersurface.
- études pratiques dans le cas où on peut paramétrer X
- Calcul différentiel d’ordre 2 :
- fonctions C^2, C^k, théorème de Schwarz (admis)
- Calcul de la dérivée seconde de t->f(a+tx)
- Définition de la Hessienne d’une fonction f : U -> R, expliquer pourquoi c’est aussi la jacobienne du gradient de f.
- Savoir citer le théorème de Taylor-Young à l’ordre 2 (admis)
- C.N. de min. local : point critique a tel que Hf(a) soit symétrique positive (savoir dém).
- C.S. de min. local : point critique a tel que Hf(a) soit définie positive. (savoir dém.)
- Pratique en dim. 2 avec det(Hf(a)) et Tr(Hf(a)).
- Exemple où Hf(a) est dégénérée (0 v.p.) en exercice.
- E.D.P. d’ordre 1 et 2 :
- savoir justement proprement la « primitivation par rapport à une variable » (convexité par rapport à la variable).
- Exemples de résolution par changement de variable.
- Tous les exercices de la Banque CCINP cité en haut de planche.
- Toutes les exercices de la planche de 1 à 18 auront été traités, (peut-être plus), la suite lundi.
- Exemple de recherches d’extrema sous-contrainte i.e. pour f_X
- Planche-F2
-
- Définition de la dérivée D_v f(a) de la fonction f selon le vecteur v au point a et lien avec les dérivées partielles, cas où f est une norme N et a=0 ?
- Savoir qu’il existe des fonctions f telles que D_v f(a) existe pour tout v et qui ne sont pourtant pas continue en a (exemple sur la planche ou en cours).uls
- Définition de la différentiabilité : existence d’un D.L. 1, définition du gradient pour les fonctions à valeurs scalaires.
- Faire BEAUCOUP de calculs de différentielle (de gradient) avec des D.L. 1 comme ceux de la planche ex 5,6,7.
- Déf. des fonctions de classe C^1 : l’application x-> df(x) est continue, mais surtout caractérisation miraculeuse avec les dérivées partielles
- Exercices concrets où l’on utilise le point précédent (cf. planche et banque CCINP).
- Formule sur la différentielle d’une composée d(f o g)=, deux cas particuliers très utiles si l’espace intermédiaire est R et surtout si l’espace de départ est R (dérivée selon une courbe à savoir par coeur !)
- Formule d’intégration le long d’un chemin. Application si df=0 sur un ouvert c.p.a. alors f est constante.
- C.N. d’extremum local en un point d’un ouvert : point critique.
- Vecteur tangent en un point x à un sous-ensemble X de R^n : définition, exemples, structure de cône de l’ensemble T_x X de ces vecteurs.
- Exemple si X est une sphère (savoir refaire) dans R^n.
- Cas général d’un point régulier x d’une hypersurface g=0 : T_x X=ker dg(x).
- Trois définitions équivalentes de la dérivabilité pour f : I -> E (dém. non demandée)
- Dérivée de L o f si f est dérivable de I dans E et L est linéaire de E dans F (dém.)
- Dérivée de B(f,g) si f (resp. g) sont dérivables de I dans E (resp. dans F) et B : E x F-> G est bilinéaire
- Extension du point précédent aux applications n-linéaires (typiquement déterminant).
- T.A.F. généralisé à deux fonctions » f'(c) (g(b)-g(a))=g'(c)(f(b)-f(a)) » démonstration vectorielle
- Dérivation de t-> exp(tA) par théorème de dérivation terme à terme à valeurs vectorielles
- Inégalité triangulaire pour les intégrales de fonctions vectorielles et application à l’I.A.F. dans l’hypothèse C^1.
- Formules de Taylor à savoir parfaitement.
- Moments d’ordre r d’une v.a.d. : si X admet un moment d’ordre r alors X admet un moment d’ordre s pour tout s<r.
- Calculs des variances des lois usuelles et notamment géométriques et Poisson et cas de loi binomiale comme sommes de v.a. indépendantes
- Covariance, application à la variance d’une somme
- Deux inégalités de Cauchy-Schwarz dans le contexte probabiliste, l’une avec la Covariance, l’une avec (X,Y)->E(XY)
- Série et fonction génératrice : deux définitions. La série génératrice détermine la loi
- Fonction génératrice d’une somme de v.a.d. indépendantes application à la loi binomiale, à la somme de deux v.a. de Poisson indépendantes
- Calcul de l’espérance (resp. de E(X^2)) en dérivant la fonction génératrice
- Inégalité de Markov et de Tchebychev, application méthode du 1er moment ou 2ème moment pour l’étude de P(X=0).
- Loi faible des grands nombres: énoncé et démonstration.
- Définir ce qu’est une tribu et exemples simples sur la planche P1.
- Qu’est-ce qu’une probabilité ? Démontrer la propriété de continuité croissante.
- Démontrer la sous-additivité dénombrable des probabilités.
- Donner des propriétés de l’espace probabilisé décrivant le jeu à pile ou face infini (où l’existence de la proba est bien sûr admise) : quelle tribu, comment montrer que la probabilité des singletons est nulle.
- Dans l’exemple précédent donner un exemple de système quasi-complet d’événements (qui n’est pas « complet »).
- Evénement « A_n est réalisé infiniment souvent » décrit avec inter et union, premier lemme de Borel-Cantelli (exercice Planche-P1)
- Définition d’une v.a.d. : savoir vérifier les conditions de la déf. d’une v.a.d : exemple du temps d’attente de succès dans une suite de tirages de Bernoulli (v.a.d. de loi géométrique).
- Caractérisation des v.a. géométriques par le caractère « sans-mémoire »
- Convergence en loi de v.a. suivant B(n,lambda/n) vers P(lambda)
- Indépendance des v.a.d. : déf. équivalentes (dém. non demandée).
- Espérance des v.a. géométriques et de Poisson.
- Propriété de l’espérance : formule de transfert, linéarité.
- Calcul de l’espérance à l’aide des P¨(X>x).
- Pour f autoadjoint, définir la forme bilinéaire symétrique associée à f (à savoir (x,y)-> (f(x)|y)), et la forme quadratique associée x->(f(x)|x). Chacun de ces trois objets détermine les autres : pourquoi ? (Formule de polarisation).
- Démontrer qu’un endomorphisme autoadjoint admet au moins une valeur propre (en se ramenant à la dim. 2).
- En admettant le résultat précédent, démontrer le théorème spectral pour les autoadjoints.
- Ecriture de la forme quadratique (mot H.P.) x-> (f(x)|x) dans une b.o.n. de dz. de f, application à une caractérisation de la plus grande et de la plus petite v.p. de f.
- Définition des autoadjoints positifs (resp. matrices symétriques positives) et caractérisation par le spectre.
- Déf. des autoadjoints définis positifs, caractérisation par le spectre, lien avec la notion de produit scalaire.
- Tous les exercices de la planche ont été traités sauf le 17 : Planche-R4
- Les exercices 10, 11, 12 de la Planche-R2
- Les exercices 4 à 8 et l’ex. 11 de la Planche-R3
- Ne pas négliger les calculs concrets : banque CCINP Ex. 68, et toujours des projections orthogonales (décidément mal comprises) CCINP Ex. 81,82, et des calculs de matrices de projections…
- Définition de l’adjoint d’un endomorphisme et prop. de l’application u-> u*
- Si F est un s.e.v. stable par u, alors l’orthogonal de F est stable par u*
- La matrice de u* dans une b.o.n. est la transposée de celle de u
- Déf. des isométries vectorielles et caractérisation par la conservation du produit scalaire et par f*=f^{-1}
- Caractérisation matricielle des isométries vectorielles et déf. des matrices orthogonale.
- Déterminant d’une matrice orthogonale. Donner une matrice de déterminant 1 non orthogonale.
- Une matrice orthogonale symétrique est une matrice de symétrie orthogonale.
- Thme de classification des matrices dans O_2(R).
- Thme de classification de toutes les isométries vectorielles : énoncé, étapes de la preuve.
- Citer le théorème d’approximation uniforme des fonctions c.p.m. par des fonctions en escalier et savoir l’appliquer pour démontrer le théorème de Riemann-Lebesgue sur un segment (thme H.P. mais à connaître aussi bien pour le résultat que pour la méthode).
- Citer le théorème d’approximation de Weierstrass et montrer qu’on ne peut pas espérer une CVU sur R entier car si une suite de polynômes CVU sur R entier….
- Savoir refaire la Q3 et le « lemme de Dirac » du TD : TD-Chap-T4-convolution-Weierstrass
- Espaces préhilbertiens : montrer que le produit scalaire (p.s.) est une forme bilinéaire continue.
- Exercice : lemme des moments :
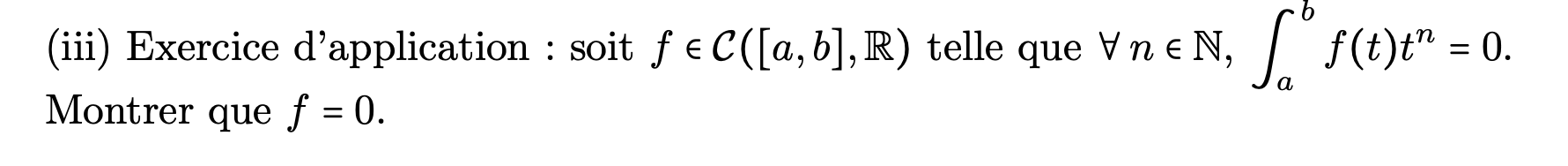
- Savoir montrer:

- Donner des exemples de sev stricts denses dans deux espaces préhilbertiens différents.
- Calcul pratique de l’orthogonalisation de Gram-Schmidt : par exemple de (1,X,X^2) pour un p.s. intégrale.
- Formule du projeté orthogonal sur F si on a une base orthogonale de F : calculs concrets.
- Théorème de meilleure approximation par le projeté orthogonal, dém (Pythagore)
- Applications concretes de ce théorème de meilleure approximation pour la minimisation d’une intégrale…. et dans le cadre matriciel cf. Banque CCINP ex. 80, 81 et 82.
- Exercice de la Planche-T4: seuls les ex. 4,5,6,7 sont « exigibles ».
- Montrer le théorème de Bolzano-Weierstrass (B.W.) dans C en admettant le résultat dans R.
- Montrer qu’un compact de E est fermé borné dans E.
- Montrer qu’un fermé dans un compact est compact.
- Donner un exemple de fermé borné non compact (aussi exercice 13 banque CCINP sur ce sujet mais penser au cadre préhilbertien aussi).
- Montrer que l’image continue d’un compact est compacte.
- Théorème des bornes atteintes pour les fonctions d’un compact dans R.
- B.W. en dim. finie : les compact d’un e.v.n. de dim. finie sont les fermés bornés.
- Montrer qu’un s.e.v. de dim. finie est toujours fermé dans tout e.v.n.
- Parties connexes par arc (c.p.a.) de R?
- Image continue d’un c.p.a.
- Connexité par arc pour montrer qu’une fonction d’un intervalle I de R dans R continue injective est strictement monotone.
- Montrer que tout ensemble infini contient un sous-ensemble dnb,
- Montrer que toute partie de N est finie ou dnb, et donc aussi toute partie d’un ensemble dnb est dnb
- Montrer que NxN est dnb et pourquoi le produit de deux ensembles dnb est dnb
- Pourquoi Q est-il dnb?
- Une union dnb d’ensembles dnb est dnb
- Un produit fini d’ensemble dnb est dnb (réc. immédiate non demandée) contre-exemple pour un produit infini, construction diagonale de Cantor.
- Déf du développement décimal ou dyadique propre de R, application à la non dnb.
- séries entières (quasiment toute la planche à été traitée, les élèves devraient donc bénéficier de plus de recul sur le sujet) : privilégier déjà les aspects calculatoires quasi « algébriques » (calculs de D.S.E., E.D., D.E.S) cf. ex. 8 à 15 de la planche S3, et pour les plus avancé.e.s. on pourra aborder les questions d’analyse plus fine (ex. 16 et suivants pl. S3).
- intégrales à paramètres : là rester simple car la pratique doit encore s’affermir, seul les 5 premiers exercices de la planche I3 sont exigibles (le 4 et 5 devant être finis pendant les vacances). Ces intégrales à paramètres reviendront sûrement pour les colles de la semaine suivante.
- Lemme d’Abel, dém. et (prop.-)-définition du rayon de convergence.
- Lemme de d’Alembert pour les séries entières : dém. avec le lemme pour les séries numériques.
- Prop. ;
 ont même rayon de convergence (au programme officiel pour alpha=1, démontrée, pour pas plus cher pour alpha qcq donc je pense qu’on peut s’en servir pour alpha quelconque).
ont même rayon de convergence (au programme officiel pour alpha=1, démontrée, pour pas plus cher pour alpha qcq donc je pense qu’on peut s’en servir pour alpha quelconque). - Rayon de convergence d’une somme et produit de Cauchy.
- Continuité de la fonction somme dans le disque ouvert de convergence.
- Pour ce qui la variable est réelle :
- Théorème de continuité radiale d’Abel : énoncé seulement, mais savoir l’appliquer sur des exemples (série harmonique alternée…)
- Dérivation terme à terme automatique pour les sommes de séries entières
- unicité des coefficients du D.S.E., série de Taylor, rigidité des fonctions D.S.E.
- DSE des fonctions usuelles : preuve de la formule du binôme (1+x)^a pour a réel avec la méthode de l’E.D.
- Banque CCINP cf haut de la planche.
- Exercice : Montrer que si I est BORNE et (f_n) est une suite de fonctions L^1 sur I qui CVU sur I vers une fonction f c.p.m. alors f est L^1 et la suite des intégrales des (f_n) CV vers celle de f (généralisation du théorème connu sur les segments au cas borné).
- Donner un exemple où le résultat précédent n’est PAS vrai avec I un intervalle non borné. Expliquer le problème.
- Application du T.C.D. avec des « bornes variables »:

- Etude des intégrales de Wallis : détermination d’un équivalent
- Méthode l’I.P.P fait sortir le terme prépondérant pour un équivalent de :
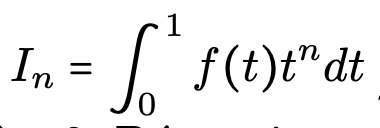
- Le même équivalent par la méthode de changement de variable.
- Intégration terme à terme d’une CVU sur un segment :
-
- application aux séries entières : montrer que :
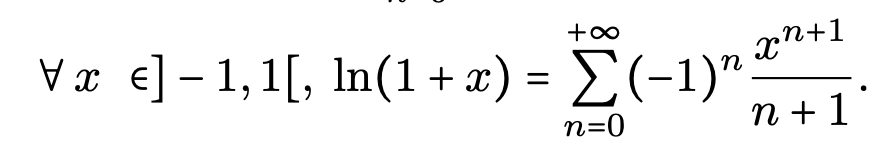
- applications aux séries trigonométriques (très important car H.P. mais dans tellement de sujets d’écrits de maths et dans le cours de physique)

- application aux séries entières : montrer que :
-
- Théorème d’intégration terme à terme de Lebesgue en deux théorèmes : cas positif et cas signe quelconque. Exemple du second cas :

- Ce qu’on fait quand le théorème ne s’applique pas. Exemple :

- Planche I2 : les exercices 1 à 4 ainsi que le 6 ont été faits en classe cette semaine. D’autres seront corrigés lundi. Planche-I2
- On pourra demander un énoncé précis de théorème en début de colle.
- Démonstration du théorème de continuité d’une limite uniforme d’une suite de fonction continue.
- Démonstration du théorème d’intégration d’une limite uniforme sur un segment.
- Le théorème d’interversion des limites a été admis.
- Exemple de la fonction zeta réelle : caractère C infini, limite à l’infini
- Exemple de la suite de fonctions x-> n sin(x/n) méthode pour la CVU sur les segments et pourquoi on n’ a pas CVU sur R
- Méthode d’encadrement par des intégrales pour un équivalent quand x->0 de la somme des exp(-x sqrt(n)).
- ouverts et fermés relatifs : définition d’un ouvert de A, d’un fermé de A, caractérisations (démo non exigibles).
- déf. de la continuité en un point et caractérisation avec les voisinages avec démonstration.
- caractérisation globale de la continuité : f est continue de A dans F ssi la préimage d’un ouvert de F est un ouvert de A (resp. d’un fermé) : démo. non exigible, par contre : savoir bien la mettre en oeuvre pour montrer que tel ensemble est ouvert ou fermé.
- Savoir justifier qu’une application donnée est continue : théorème d’opération, continuité des formes coordonnées, et donc des fonctions polynomiales ou rationnelles.
- Une fonction à valeur dans K^n est continue ssi ses composantes le sont (dém).
- Justifier la continuité de l’application A -> A¨^{-1} sur GL¨_n(K).
- Définir ce qu’est un homéomorphisme et pourquoi l’image d’un ouvert par un homéo est un ouvert.
- Montrer que x-> d(x,A) est 1 -lipschitzienne.
- Caractérisation de la continuité des applications linéaires : 5 conditions, avec dém.
- Définition de la norme d’opérateur (trois formules équivalentes).
- Calcul pratique de cette norme sur des exemples (cf. ex CCINP 37).
- Montrer que la norme infinie sur l’espace des fonctions bornées est bien une norme (on sera très précis pour les arguments sur les sup.)
- définir ce qu’est une norme d’algèbre, en donner des exemples dans l’algèbre des fonctions bornées, et dans l’algèbre des matrices carrées.
- Théorème pour les produits de limites de suites dans une algèbre normée.
- Justifier que dans un evn de dim. finie, la convergence d’une suite se vérifie « coordonnée par coordonnée ».
- Justifier que dans un evn de dim. finie, une série absolument convergente est convergente.
- Justification de l’existence de l’exp. matricielle.
- Montrer qu’une boule ouverte est ouverte, une boule fermée est fermée.
- Montrer que l’intérieur d’une boule fermée est la boule ouverte
- Montrer que l’adhérence d’une boule ouverte est la boule fermée
- Montrer qu’un s.e.v. strict est d’intérieur vide.
- Caractérisation séquentielle des points adhérence.
- Lien complémentaire de l’adhérence/intérieur du complémentaire..
- Trigonalisation : démonstration par récurrence du théorème qui dit qu’un endomorphisme ayant polynôme annulateur scindé est tz.
- Caractérisations des nilpotents en termes de v.p. dans C et autre (des équivalences très simples !)
- Les élèves doivent savoir conduire la trigonalisation concrète d’une matrice 2x 2, et d’une matrice 3 x 3 et même la réduction sous forme de Jordan dans ces cas particuliers (deux cas en dim. 3…)
- Théorème de décomposition sur les s.e.v. caractéristiques : donne une tz précisée.
- Calcul du polynôme caractéristique d’une matrice compagnon.
- Justifier que la multiplicité géométrique d’une v.p. est inférieure ou égale à sa multiplicité algébrique.
- Révisions sur les formules de changement de base, pour les vecteurs et les applications linéaires.
- valeurs propres, vecteurs propres : recherche à l’aide de l’équation aux valeurs propres sur des exemples en dim. finie ou infinie
- caractérisation : lambda v.p. d’une matrice A ssi det(A-lambda I)=0, application aux v.p. des matrices triangulaires
- Démonstration(s) du fait que des s.e.v. propres associés à des v.p. distinctes sont en somme directe
- Si lambda est v.p. d’un endomorphisme L et si P est un polynôme alors P(lambda) est v.p. de P(L). Conséquence si P est annulateur de L
- Les v.p. de L sont exactement les racines du polynôme minimal de L.
- Théorème de décomposition des noyaux : démonstration pour un produit de deux polynômes. On sera spécialement attentif à la bonne compréhension des objets manipulés (P(L)(x) et pas P(L(x)) et (PQ)(L)=P(L)o Q(L) etc…)
- Savoir donner le maximum de caractérisation d’une matrice diagonalisable et la C.S. « n v.p. distinctes en dim. n « .
- Toute la Planche-R0 a été faite en classe. On pourra demander de retraiter un exercice de cette planche en question de cours.
- On pourra aussi vérifier la connaissance des théorèmes de première année : par exemple, les théorèmes sur le rang (notion dont je me suis aperçu qu’elle était mal connue) !
-
- caractérisation du rang avec les matrices extraites,
- le fait que toute matrice de rang r soit équivalente à une matrice ‘J_r’,
- ou encore qu’une matrice et sa transposée ont le même rang.
-
- Le cours de la semaine : Arithmétique/Polynôme et Polynômes appliqués à des matrices.
Question sur cours :
- savoir définir un idéal et savoir pourquoi les idéaux de K[X] sont principaux,
- savoir la prop-définition du PGCD et PPCM avec les idéaux et pourquoi cette déf entraîne immédiatement que tout multiple commun est un multiple du PPCM et tout diviseur commun est un diviseur du PGCD
- Savoir la caractérisation des éléments inversibles dans Z/nZ.
- Propriété définition du polynôme minimal d’une matrice, d’un endomorphisme.
- Connaitre le polynôme minimal d’une matrice diagonale.
- Savoir pourquoi l’inverse d’une matrice A est un polynôme en A.
- Savoir pourquoi P(A) inversible dans M_n(K) ssi P et mu_A sont premiers entre eux.
- Définition de la divergence grossière, et savoir démontrer que si la série de terme général (u_n) converge alors (u_n) tend vers zéro.
- Test de d’Alembert avec démonstration.
- Sur la comparaison série/intégrale, pour les colleurs le programme officiel a un peu changé il s’agit maintenant plus d’un savoir faire que d’un résultat, savoir justifier le D.A. de H_n à la précision o(1).
- Citer précisément le théorème de sommation des relations de comparaison et démontrer un cas.
- Citer le Théorème spécial pour certaines séries alternées avec comme conclusion aussi le signe du reste et la majoration du reste.
- Savoir mettre en oeuvre le lien suites/séries pour gagner un terme supplémentaire dans le D.A. de H_n. (précision o(1/n)).
- Révisions sur les formules de changement de base, pour les vecteurs et les applications linéaires.
- valeurs propres, vecteurs propres : recherche à l’aide de l’équation aux valeurs propres sur des exemples en dim. finie ou infinie
- caractérisation : lambda v.p. d’une matrice A ssi det(A-lambda I)=0, application aux v.p. des matrices triangulaires
- Démonstration(s) du fait que des s.e.v. propres associés à des v.p. distinctes sont en somme directe
- Si lambda est v.p. d’un endomorphisme L et si P est un polynôme alors P(lambda) est v.p. de P(L). Conséquence si P est annulateur de L
- Les v.p. de L sont exactement les racines du polynôme minimal de L.
- Théorème de décomposition des noyaux : démonstration pour un produit de deux polynômes. On sera spécialement attentif à la bonne compréhension des objets manipulés (P(L)(x) et pas P(L(x)) et (PQ)(L)=P(L)o Q(L) etc…)
- Savoir donner le maximum de caractérisation d’une matrice diagonalisable et la C.S. « n v.p. distinctes en dim. n « .
- Toute la Planche-R0 a été faite en classe. On pourra demander de retraiter un exercice de cette planche en question de cours.
- On pourra aussi vérifier la connaissance des théorèmes de première année : par exemple, les théorèmes sur le rang (notion dont je me suis aperçu qu’elle était mal connue) !
-
- caractérisation du rang avec les matrices extraites,
- le fait que toute matrice de rang r soit équivalente à une matrice ‘J_r’,
- ou encore qu’une matrice et sa transposée ont le même rang.
-
- Le cours de la semaine : Arithmétique/Polynôme et Polynômes appliqués à des matrices.
Question sur cours :
- savoir définir un idéal et savoir pourquoi les idéaux de K[X] sont principaux,
- savoir la prop-définition du PGCD et PPCM avec les idéaux et pourquoi cette déf entraîne immédiatement que tout multiple commun est un multiple du PPCM et tout diviseur commun est un diviseur du PGCD
- Savoir la caractérisation des éléments inversibles dans Z/nZ.
- Propriété définition du polynôme minimal d’une matrice, d’un endomorphisme.
- Connaitre le polynôme minimal d’une matrice diagonale.
- Savoir pourquoi l’inverse d’une matrice A est un polynôme en A.
- Savoir pourquoi P(A) inversible dans M_n(K) ssi P et mu_A sont premiers entre eux.
- Définition de la divergence grossière, et savoir démontrer que si la série de terme général (u_n) converge alors (u_n) tend vers zéro.
- Test de d’Alembert avec démonstration.
- Sur la comparaison série/intégrale, pour les colleurs le programme officiel a un peu changé il s’agit maintenant plus d’un savoir faire que d’un résultat, savoir justifier le D.A. de H_n à la précision o(1).
- Citer précisément le théorème de sommation des relations de comparaison et démontrer un cas.
- Citer le Théorème spécial pour certaines séries alternées avec comme conclusion aussi le signe du reste et la majoration du reste.
- Savoir mettre en oeuvre le lien suites/séries pour gagner un terme supplémentaire dans le D.A. de H_n. (précision o(1/n)).
- ouverts et fermés relatifs : définition d’un ouvert de A, d’un fermé de A, caractérisations (démo non exigibles).
- déf. de la continuité en un point et caractérisation avec les voisinages avec démonstration.
- caractérisation globale de la continuité : f est continue de A dans F ssi la préimage d’un ouvert de F est un ouvert de A (resp. d’un fermé) : démo. non exigible, par contre : savoir bien la mettre en oeuvre pour montrer que tel ensemble est ouvert ou fermé.
- Savoir justifier qu’une application donnée est continue : théorème d’opération, continuité des formes coordonnées, et donc des fonctions polynomiales ou rationnelles.
- Une fonction à valeur dans K^n est continue ssi ses composantes le sont (dém).
- Justifier la continuité de l’application A -> A¨^{-1} sur GL¨_n(K).
- Définir ce qu’est un homéomorphisme et pourquoi l’image d’un ouvert par un homéo est un ouvert.
- Montrer que x-> d(x,A) est 1 -lipschitzienne.
- Caractérisation de la continuité des applications linéaires : 5 conditions, avec dém.
- Définition de la norme d’opérateur (trois formules équivalentes).
- Calcul pratique de cette norme sur des exemples (cf. ex CCINP 37).
- Montrer que la norme infinie sur l’espace des fonctions bornées est bien une norme (on sera très précis pour les arguments sur les sup.)
- définir ce qu’est une norme d’algèbre, en donner des exemples dans l’algèbre des fonctions bornées, et dans l’algèbre des matrices carrées.
- Théorème pour les produits de limites de suites dans une algèbre normée.
- Justifier que dans un evn de dim. finie, la convergence d’une suite se vérifie « coordonnée par coordonnée ».
- Justifier que dans un evn de dim. finie, une série absolument convergente est convergente.
- Justification de l’existence de l’exp. matricielle.
- Montrer qu’une boule ouverte est ouverte, une boule fermée est fermée.
- Montrer que l’intérieur d’une boule fermée est la boule ouverte
- Montrer que l’adhérence d’une boule ouverte est la boule fermée
- Montrer qu’un s.e.v. strict est d’intérieur vide.
- Caractérisation séquentielle des points adhérence.
- Lien complémentaire de l’adhérence/intérieur du complémentaire..
- Trigonalisation : démonstration par récurrence du théorème qui dit qu’un endomorphisme ayant polynôme annulateur scindé est tz.
- Caractérisations des nilpotents en termes de v.p. dans C et autre (des équivalences très simples !)
- Les élèves doivent savoir conduire la trigonalisation concrète d’une matrice 2x 2, et d’une matrice 3 x 3 et même la réduction sous forme de Jordan dans ces cas particuliers (deux cas en dim. 3…)
- Théorème de décomposition sur les s.e.v. caractéristiques : donne une tz précisée.
- Calcul du polynôme caractéristique d’une matrice compagnon.
- Justifier que la multiplicité géométrique d’une v.p. est inférieure ou égale à sa multiplicité algébrique.
- Révisions sur les formules de changement de base, pour les vecteurs et les applications linéaires.
- valeurs propres, vecteurs propres : recherche à l’aide de l’équation aux valeurs propres sur des exemples en dim. finie ou infinie
- caractérisation : lambda v.p. d’une matrice A ssi det(A-lambda I)=0, application aux v.p. des matrices triangulaires
- Démonstration(s) du fait que des s.e.v. propres associés à des v.p. distinctes sont en somme directe
- Si lambda est v.p. d’un endomorphisme L et si P est un polynôme alors P(lambda) est v.p. de P(L). Conséquence si P est annulateur de L
- Les v.p. de L sont exactement les racines du polynôme minimal de L.
- Théorème de décomposition des noyaux : démonstration pour un produit de deux polynômes. On sera spécialement attentif à la bonne compréhension des objets manipulés (P(L)(x) et pas P(L(x)) et (PQ)(L)=P(L)o Q(L) etc…)
- Savoir donner le maximum de caractérisation d’une matrice diagonalisable et la C.S. « n v.p. distinctes en dim. n « .
- Toute la Planche-R0 a été faite en classe. On pourra demander de retraiter un exercice de cette planche en question de cours.
- On pourra aussi vérifier la connaissance des théorèmes de première année : par exemple, les théorèmes sur le rang (notion dont je me suis aperçu qu’elle était mal connue) !
-
- caractérisation du rang avec les matrices extraites,
- le fait que toute matrice de rang r soit équivalente à une matrice ‘J_r’,
- ou encore qu’une matrice et sa transposée ont le même rang.
-
- Le cours de la semaine : Arithmétique/Polynôme et Polynômes appliqués à des matrices.
Question sur cours :
- savoir définir un idéal et savoir pourquoi les idéaux de K[X] sont principaux,
- savoir la prop-définition du PGCD et PPCM avec les idéaux et pourquoi cette déf entraîne immédiatement que tout multiple commun est un multiple du PPCM et tout diviseur commun est un diviseur du PGCD
- Savoir la caractérisation des éléments inversibles dans Z/nZ.
- Propriété définition du polynôme minimal d’une matrice, d’un endomorphisme.
- Connaitre le polynôme minimal d’une matrice diagonale.
- Savoir pourquoi l’inverse d’une matrice A est un polynôme en A.
- Savoir pourquoi P(A) inversible dans M_n(K) ssi P et mu_A sont premiers entre eux.
- Définition de la divergence grossière, et savoir démontrer que si la série de terme général (u_n) converge alors (u_n) tend vers zéro.
- Test de d’Alembert avec démonstration.
- Sur la comparaison série/intégrale, pour les colleurs le programme officiel a un peu changé il s’agit maintenant plus d’un savoir faire que d’un résultat, savoir justifier le D.A. de H_n à la précision o(1).
- Citer précisément le théorème de sommation des relations de comparaison et démontrer un cas.
- Citer le Théorème spécial pour certaines séries alternées avec comme conclusion aussi le signe du reste et la majoration du reste.
- Savoir mettre en oeuvre le lien suites/séries pour gagner un terme supplémentaire dans le D.A. de H_n. (précision o(1/n)).
- Révisions sur les formules de changement de base, pour les vecteurs et les applications linéaires.
- valeurs propres, vecteurs propres : recherche à l’aide de l’équation aux valeurs propres sur des exemples en dim. finie ou infinie
- caractérisation : lambda v.p. d’une matrice A ssi det(A-lambda I)=0, application aux v.p. des matrices triangulaires
- Démonstration(s) du fait que des s.e.v. propres associés à des v.p. distinctes sont en somme directe
- Si lambda est v.p. d’un endomorphisme L et si P est un polynôme alors P(lambda) est v.p. de P(L). Conséquence si P est annulateur de L
- Les v.p. de L sont exactement les racines du polynôme minimal de L.
- Théorème de décomposition des noyaux : démonstration pour un produit de deux polynômes. On sera spécialement attentif à la bonne compréhension des objets manipulés (P(L)(x) et pas P(L(x)) et (PQ)(L)=P(L)o Q(L) etc…)
- Savoir donner le maximum de caractérisation d’une matrice diagonalisable et la C.S. « n v.p. distinctes en dim. n « .
- Toute la Planche-R0 a été faite en classe. On pourra demander de retraiter un exercice de cette planche en question de cours.
- On pourra aussi vérifier la connaissance des théorèmes de première année : par exemple, les théorèmes sur le rang (notion dont je me suis aperçu qu’elle était mal connue) !
-
- caractérisation du rang avec les matrices extraites,
- le fait que toute matrice de rang r soit équivalente à une matrice ‘J_r’,
- ou encore qu’une matrice et sa transposée ont le même rang.
-
- Le cours de la semaine : Arithmétique/Polynôme et Polynômes appliqués à des matrices.
Question sur cours :
- savoir définir un idéal et savoir pourquoi les idéaux de K[X] sont principaux,
- savoir la prop-définition du PGCD et PPCM avec les idéaux et pourquoi cette déf entraîne immédiatement que tout multiple commun est un multiple du PPCM et tout diviseur commun est un diviseur du PGCD
- Savoir la caractérisation des éléments inversibles dans Z/nZ.
- Propriété définition du polynôme minimal d’une matrice, d’un endomorphisme.
- Connaitre le polynôme minimal d’une matrice diagonale.
- Savoir pourquoi l’inverse d’une matrice A est un polynôme en A.
- Savoir pourquoi P(A) inversible dans M_n(K) ssi P et mu_A sont premiers entre eux.
- Définition de la divergence grossière, et savoir démontrer que si la série de terme général (u_n) converge alors (u_n) tend vers zéro.
- Test de d’Alembert avec démonstration.
- Sur la comparaison série/intégrale, pour les colleurs le programme officiel a un peu changé il s’agit maintenant plus d’un savoir faire que d’un résultat, savoir justifier le D.A. de H_n à la précision o(1).
- Citer précisément le théorème de sommation des relations de comparaison et démontrer un cas.
- Citer le Théorème spécial pour certaines séries alternées avec comme conclusion aussi le signe du reste et la majoration du reste.
- Savoir mettre en oeuvre le lien suites/séries pour gagner un terme supplémentaire dans le D.A. de H_n. (précision o(1/n)).
- Révisions sur les formules de changement de base, pour les vecteurs et les applications linéaires.
- valeurs propres, vecteurs propres : recherche à l’aide de l’équation aux valeurs propres sur des exemples en dim. finie ou infinie
- caractérisation : lambda v.p. d’une matrice A ssi det(A-lambda I)=0, application aux v.p. des matrices de petites tailles et des matrices triangulaires
- Démonstration du fait que des s.e.v. propres associés à des v.p. distinctes sont en somme directe
- Si lambda est v.p. d’un endomorphisme L et si P est un polynôme alors P(lambda) est v.p. de P(L). Conséquence si P est annulateur de L, Sp(L) est inclus dans Z(P).
- Les v.p. de L sont exactement les racines du polynôme minimal de L.
- Théorème de décomposition des noyaux : démonstration pour un produit de deux polynômes. On sera spécialement attentif à la bonne compréhension des objets manipulés (P(L)(x) et pas P(L(x)) et (PQ)(L)=P(L)o Q(L) etc…)
- Savoir donner le maximum de caractérisations d’une matrice diagonalisable et la C.S. « n v.p. distinctes en dim. n » mais en fait retenir surtout et pour chaque exercice qu’il y a d »un côté le point de vue géométrique (avec les vecteurs propres et les ses propres) et le point de vue algébrique (avec les polynômes annulateurs, le minimal;
- Qu’est-ce qu’un anneau, qu’est-ce corps ? Montrer que Z/nZ est un corps ssi Z/nZ est intègre ssi n est un nombre premier.
- Plus généralement : pour a dans Z, montrer que la classe de a est inversible dans l’anneau Z/nZ ssi a et n sont premiers entre eux
- savoir définir ce qu’est un idéal et savoir la forme des idéaux de K[X] et de Z (dém. sur K[X]).
- Définir le polynôme minimal d’un matrice (resp. d’un endomorphisme d’un e.v. de dim. finie) et savoir pourquoi tout polynôme annulateur est divisible par le polynôme minimal.
- Expliciter le polynôme minimal d’une matrice diagonale.
- Montrer que dim K[A]=deg(mu_A).
- Montrer que si A est une matrice inversible alors A^{-1} est dans K[A].
- Montrer que si A est une matrice et P est un polynôme alors P(A) est une matrice inversible ssi P est premier avec le polynôme minimal de A.
- Somme directe de plusieurs s.e.v.: définitions, différentes caractérisations
- Matrices par blocs : produits, opérations élémentaires sur les blocs, formule du déterminant d’une matrice triangulaire par bloc (deux démonstrations).
- Définition de la divergence grossière, et savoir démontrer que si la série de terme général (u_n) converge alors (u_n) tend vers zéro.
- Test de d’Alembert avec démonstration.
- Sur la comparaison série/intégrale, pour les colleurs le programme officiel a un peu changé il s’agit maintenant plus d’un savoir faire que d’un résultat, savoir justifier le D.A. de H_n à la précision o(1).
- Citer précisément le théorème de sommation des relations de comparaison et démontrer un cas.
- Citer le Théorème spécial pour certaines séries alternées avec comme conclusion aussi le signe du reste et la majoration du reste.
- Savoir mettre en oeuvre le lien suites/séries pour gagner un terme supplémentaire dans le D.A. de H_n. (précision o(1/n)) ou donner l’idée de la preuve de la formule de Stirling et en faire une ou deux étapes.
- Révisions sur les suites récurrentes u_{n+1}=f(u_n) ou les suites définies
- Familles sommables : savoir bien distinguer entre le cas positifs et le cas à signe variable/complexe. Savoir bien mettre en oeuvre le théorème de sommation terme par paquets sans justification particulière que la positivité dans le cas positif, et au contraire avec justification préalable de la sommabilité dans le cas général.. justement avec le T.S.P. positif.
Banque CCINP ex 1 à 20 et 59 à 76. (Ne tardez pas à réviser ces exercices CCINP vous devez les connaître sur les bouts des doigts).
Pour la semaine du 30 mai au 2 juin : ex 1 à 25 et 50 à 83.
Pour la semaine du 5 juin au 10 juin : ex 1 à 45 et 50 à 94.
A partir du 12 juin : toute la banque.
Semaine 23 : du lundi 27 mars
Attention : dernière semaine de colles avant les écrits.
Thème : calcul différentiel, révision du programme précédent et les rajouts qui suivent. Par ailleurs, on peut aussi poser des questions de révisions sur les endomorphismes d’un espace euclidien.
Calcul diff. on rajoute :
-
- Exemple de recherches d’extrema sous-contrainte i.e. pour f_X
- théorème dans le cas où X est une hypersurface.
- études pratiques dans le cas où on peut paramétrer X
- Calcul différentiel d’ordre 2 :
- fonctions C^2, C^k, théorème de Schwarz (admis)
- Calcul de la dérivée seconde de t->f(a+tx)
- Définition de la Hessienne d’une fonction f : U -> R, expliquer pourquoi c’est aussi la jacobienne du gradient de f.
- Savoir citer le théorème de Taylor-Young à l’ordre 2 (admis)
- C.N. de min. local : point critique a tel que Hf(a) soit symétrique positive (savoir dém).
- C.S. de min. local : point critique a tel que Hf(a) soit définie positive. (savoir dém.)
- Pratique en dim. 2 avec det(Hf(a)) et Tr(Hf(a)).
- Exemple où Hf(a) est dégénérée (0 v.p.) en exercice.
- E.D.P. d’ordre 1 et 2 :
- savoir justement proprement la « primitivation par rapport à une variable » (convexité par rapport à la variable).
- Exemples de résolution par changement de variable.
- Tous les exercices de la Banque CCINP cité en haut de planche.
- Toutes les exercices de la planche de 1 à 18 auront été traités, (peut-être plus), la suite lundi.
- Exemple de recherches d’extrema sous-contrainte i.e. pour f_X
- Planche-F2
-
- Définition de la dérivée D_v f(a) de la fonction f selon le vecteur v au point a et lien avec les dérivées partielles, cas où f est une norme N et a=0 ?
- Savoir qu’il existe des fonctions f telles que D_v f(a) existe pour tout v et qui ne sont pourtant pas continue en a (exemple sur la planche ou en cours).
- Définition de la différentiabilité : existence d’un D.L. 1, définition du gradient pour les fonctions à valeurs scalaires.
- Faire BEAUCOUP de calculs de différentielle (de gradient) avec des D.L. 1 comme ceux de la planche ex 5,6,7.
- Déf. des fonctions de classe C^1 : l’application x-> df(x) est continue, mais surtout caractérisation miraculeuse avec les dérivées partielles
- Exercices concrets où l’on utilise le point précédent (cf. planche et banque CCINP).
- Formule sur la différentielle d’une composée d(f o g)=, deux cas particuliers très utiles si l’espace intermédiaire est R et surtout si l’espace de départ est R (dérivée selon une courbe à savoir par coeur !)
- Formule d’intégration le long d’un chemin. Application si df=0 sur un ouvert c.p.a. alors f est constante.
- C.N. d’extremum local en un point d’un ouvert : point critique.
- Vecteur tangent en un point x à un sous-ensemble Xde R^n : définition, exemples, structure de cône de l’ensemble T_x X de ces vecteurs.
- Exemple si X est une sphère (savoir refaire) dans R^n.
- Cas général d’un point régulier x d’une hypersurface g=0 : T_x X=ker dg(x).
- Trois définitions équivalentes de la dérivabilité pour f : I -> E (dém. non demandée)
- Dérivée de L o f si f est dérivable de I dans E et L est linéaire de E dans F (dém.)
- Dérivée de B(f,g) si f (resp. g) sont dérivables de I dans E (resp. dans F) et B : E x F-> G est bilinéaire
- Extension du point précédent aux applications n-linéaires (typiquement déterminant).
- T.A.F. généralisé à deux fonctions » f'(c) (g(b)-g(a))=g'(c)(f(b)-f(a)) » démonstration vectorielle
- Dérivation de t-> exp(tA) par théorème de dérivation terme à terme à valeurs vectorielles
- Inégalité triangulaire pour les intégrales de fonctions vectorielles et application à l’I.A.F. dans l’hypothèse C^1.
- Formules de Taylor à savoir parfaitement.
- Moments d’ordre r d’une v.a.d. : si X admet un moment d’ordre r alors X admet un moment d’ordre s pour tout s<r.
- Calculs des variances des lois usuelles et notamment géométriques et Poisson et cas de loi binomiale comme sommes de v.a. indépendantes
- Covariance, application à la variance d’une somme
- Deux inégalités de Cauchy-Schwarz dans le contexte probabiliste, l’une avec la Covariance, l’une avec (X,Y)->E(XY)
- Série et fonction génératrice : deux définitions. La série génératrice détermine la loi
- Fonction génératrice d’une somme de v.a.d. indépendantes application à la loi binomiale, à la somme de deux v.a. de Poisson indépendantes
- Calcul de l’espérance (resp. de E(X^2)) en dérivant la fonction génératrice
- Inégalité de Markov et de Tchebychev, application méthode du 1er moment ou 2ème moment pour l’étude de P(X=0).
- Loi faible des grands nombres: énoncé et démonstration.
- Définir ce qu’est une tribu et exemples simples sur la planche P1.
- Qu’est-ce qu’une probabilité ? Démontrer la propriété de continuité croissante.
- Démontrer la sous-additivité dénombrable des probabilités.
- Donner des propriétés de l’espace probabilisé décrivant le jeu à pile ou face infini (où l’existence de la proba est bien sûr admise) : quelle tribu, comment montrer que la probabilité des singletons est nulle.
- Dans l’exemple précédent donner un exemple de système quasi-complet d’événements (qui n’est pas « complet »).
- Evénement « A_n est réalisé infiniment souvent » décrit avec inter et union, premier lemme de Borel-Cantelli (exercice Planche-P1)
- Définition d’une v.a.d. : savoir vérifier les conditions de la déf. d’une v.a.d : exemple du temps d’attente de succès dans une suite de tirages de Bernoulli (v.a.d. de loi géométrique).
- Caractérisation des v.a. géométriques par le caractère « sans-mémoire »
- Convergence en loi de v.a. suivant B(n,lambda/n) vers P(lambda)
- Indépendance des v.a.d. : déf. équivalentes (dém. non demandée).
- Espérance des v.a. géométriques et de Poisson.
- Propriété de l’espérance : formule de transfert, linéarité.
- Calcul de l’espérance à l’aide des P¨(X>x).
- Pour f autoadjoint, définir la forme bilinéaire symétrique associée à f (à savoir (x,y)-> (f(x)|y)), et la forme quadratique associée x->(f(x)|x). Chacun de ces trois objets détermine les autres : pourquoi ? (Formule de polarisation).
- Démontrer qu’un endomorphisme autoadjoint admet au moins une valeur propre (en se ramenant à la dim. 2).
- En admettant le résultat précédent, démontrer le théorème spectral pour les autoadjoints.
- Ecriture de la forme quadratique (mot H.P.) x-> (f(x)|x) dans une b.o.n. de dz. de f, application à une caractérisation de la plus grande et de la plus petite v.p. de f.
- Définition des autoadjoints positifs (resp. matrices symétriques positives) et caractérisation par le spectre.
- Déf. des autoadjoints définis positifs, caractérisation par le spectre, lien avec la notion de produit scalaire.
- Tous les exercices de la planche ont été traités sauf le 17 : Planche-R4
- Les exercices 10, 11, 12 de la Planche-R2
- Les exercices 4 à 8 et l’ex. 11 de la Planche-R3
- Ne pas négliger les calculs concrets : banque CCINP Ex. 68, et toujours des projections orthogonales (décidément mal comprises) CCINP Ex. 81,82, et des calculs de matrices de projections…
- Définition de l’adjoint d’un endomorphisme et prop. de l’application u-> u*
- Si F est un s.e.v. stable par u, alors l’orthogonal de F est stable par u*
- La matrice de u* dans une b.o.n. est la transposée de celle de u
- Déf. des isométries vectorielles et caractérisation par la conservation du produit scalaire et par f*=f^{-1}
- Caractérisation matricielle des isométries vectorielles et déf. des matrices orthogonale.
- Déterminant d’une matrice orthogonale. Donner une matrice de déterminant 1 non orthogonale.
- Une matrice orthogonale symétrique est une matrice de symétrie orthogonale.
- Thme de classification des matrices dans O_2(R).
- Thme de classification de toutes les isométries vectorielles : énoncé, étapes de la preuve.
- Citer le théorème d’approximation uniforme des fonctions c.p.m. par des fonctions en escalier et savoir l’appliquer pour démontrer le théorème de Riemann-Lebesgue sur un segment (thme H.P. mais à connaître aussi bien pour le résultat que pour la méthode).
- Citer le théorème d’approximation de Weierstrass et montrer qu’on ne peut pas espérer une CVU sur R entier car si une suite de polynômes CVU sur R entier….
- Savoir refaire la Q3 et le « lemme de Dirac » du TD : TD-Chap-T4-convolution-Weierstrass
- Espaces préhilbertiens : montrer que le produit scalaire (p.s.) est une forme bilinéaire continue.
- Exercice : lemme des moments :
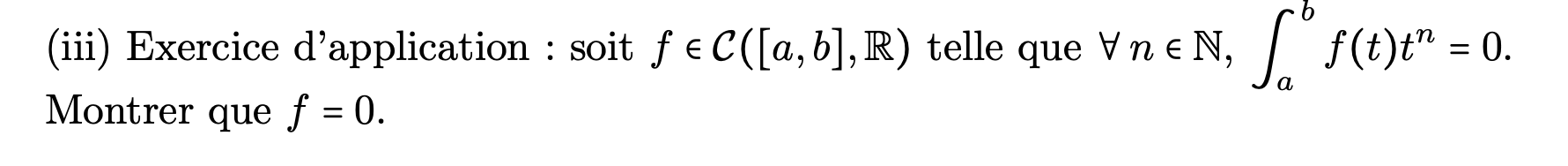
- Savoir montrer:

- Donner des exemples de sev stricts denses dans deux espaces préhilbertiens différents.
- Calcul pratique de l’orthogonalisation de Gram-Schmidt : par exemple de (1,X,X^2) pour un p.s. intégrale.
- Formule du projeté orthogonal sur F si on a une base orthogonale de F : calculs concrets.
- Théorème de meilleure approximation par le projeté orthogonal, dém (Pythagore)
- Applications concretes de ce théorème de meilleure approximation pour la minimisation d’une intégrale…. et dans le cadre matriciel cf. Banque CCINP ex. 80, 81 et 82.
- Exercice de la Planche-T4: seuls les ex. 4,5,6,7 sont « exigibles ».
- Montrer le théorème de Bolzano-Weierstrass (B.W.) dans C en admettant le résultat dans R.
- Montrer qu’un compact de E est fermé borné dans E.
- Montrer qu’un fermé dans un compact est compact.
- Donner un exemple de fermé borné non compact (aussi exercice 13 banque CCINP sur ce sujet mais penser au cadre préhilbertien aussi).
- Montrer que l’image continue d’un compact est compacte.
- Théorème des bornes atteintes pour les fonctions d’un compact dans R.
- B.W. en dim. finie : les compact d’un e.v.n. de dim. finie sont les fermés bornés.
- Montrer qu’un s.e.v. de dim. finie est toujours fermé dans tout e.v.n.
- Parties connexes par arc (c.p.a.) de R?
- Image continue d’un c.p.a.
- Connexité par arc pour montrer qu’une fonction d’un intervalle I de R dans R continue injective est strictement monotone.
- Montrer que tout ensemble infini contient un sous-ensemble dnb,
- Montrer que toute partie de N est finie ou dnb, et donc aussi toute partie d’un ensemble dnb est dnb
- Montrer que NxN est dnb et pourquoi le produit de deux ensembles dnb est dnb
- Pourquoi Q est-il dnb?
- Une union dnb d’ensembles dnb est dnb
- Un produit fini d’ensemble dnb est dnb (réc. immédiate non demandée) contre-exemple pour un produit infini, construction diagonale de Cantor.
- Déf du développement décimal ou dyadique propre de R, application à la non dnb.
- séries entières (quasiment toute la planche à été traitée, les élèves devraient donc bénéficier de plus de recul sur le sujet) : privilégier déjà les aspects calculatoires quasi « algébriques » (calculs de D.S.E., E.D., D.E.S) cf. ex. 8 à 15 de la planche S3, et pour les plus avancé.e.s. on pourra aborder les questions d’analyse plus fine (ex. 16 et suivants pl. S3).
- intégrales à paramètres : là rester simple car la pratique doit encore s’affermir, seul les 5 premiers exercices de la planche I3 sont exigibles (le 4 et 5 devant être finis pendant les vacances). Ces intégrales à paramètres reviendront sûrement pour les colles de la semaine suivante.
- Lemme d’Abel, dém. et (prop.-)-définition du rayon de convergence.
- Lemme de d’Alembert pour les séries entières : dém. avec le lemme pour les séries numériques.
- Prop. ;
 ont même rayon de convergence (au programme officiel pour alpha=1, démontrée, pour pas plus cher pour alpha qcq donc je pense qu’on peut s’en servir pour alpha quelconque).
ont même rayon de convergence (au programme officiel pour alpha=1, démontrée, pour pas plus cher pour alpha qcq donc je pense qu’on peut s’en servir pour alpha quelconque). - Rayon de convergence d’une somme et produit de Cauchy.
- Continuité de la fonction somme dans le disque ouvert de convergence.
- Pour ce qui la variable est réelle :
- Théorème de continuité radiale d’Abel : énoncé seulement, mais savoir l’appliquer sur des exemples (série harmonique alternée…)
- Dérivation terme à terme automatique pour les sommes de séries entières
- unicité des coefficients du D.S.E., série de Taylor, rigidité des fonctions D.S.E.
- DSE des fonctions usuelles : preuve de la formule du binôme (1+x)^a pour a réel avec la méthode de l’E.D.
- Banque CCINP cf haut de la planche.
- Exercice : Montrer que si I est BORNE et (f_n) est une suite de fonctions L^1 sur I qui CVU sur I vers une fonction f c.p.m. alors f est L^1 et la suite des intégrales des (f_n) CV vers celle de f (généralisation du théorème connu sur les segments au cas borné).
- Donner un exemple où le résultat précédent n’est PAS vrai avec I un intervalle non borné. Expliquer le problème.
- Application du T.C.D. avec des « bornes variables »:

- Etude des intégrales de Wallis : détermination d’un équivalent
- Méthode l’I.P.P fait sortir le terme prépondérant pour un équivalent de :
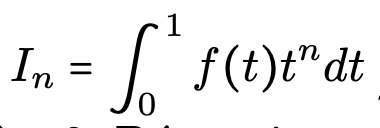
- Le même équivalent par la méthode de changement de variable.
- Intégration terme à terme d’une CVU sur un segment :
-
- application aux séries entières : montrer que :
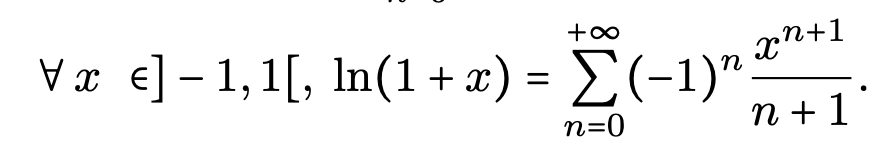
- applications aux séries trigonométriques (très important car H.P. mais dans tellement de sujets d’écrits de maths et dans le cours de physique)

- application aux séries entières : montrer que :
-
- Théorème d’intégration terme à terme de Lebesgue en deux théorèmes : cas positif et cas signe quelconque. Exemple du second cas :

- Ce qu’on fait quand le théorème ne s’applique pas. Exemple :

- Planche I2 : les exercices 1 à 4 ainsi que le 6 ont été faits en classe cette semaine. D’autres seront corrigés lundi. Planche-I2
- On pourra demander un énoncé précis de théorème en début de colle.
- Démonstration du théorème de continuité d’une limite uniforme d’une suite de fonction continue.
- Démonstration du théorème d’intégration d’une limite uniforme sur un segment.
- Le théorème d’interversion des limites a été admis.
- Exemple de la fonction zeta réelle : caractère C infini, limite à l’infini
- Exemple de la suite de fonctions x-> n sin(x/n) méthode pour la CVU sur les segments et pourquoi on n’ a pas CVU sur R
- Méthode d’encadrement par des intégrales pour un équivalent quand x->0 de la somme des exp(-x sqrt(n)).
- ouverts et fermés relatifs : définition d’un ouvert de A, d’un fermé de A, caractérisations (démo non exigibles).
- déf. de la continuité en un point et caractérisation avec les voisinages avec démonstration.
- caractérisation globale de la continuité : f est continue de A dans F ssi la préimage d’un ouvert de F est un ouvert de A (resp. d’un fermé) : démo. non exigible, par contre : savoir bien la mettre en oeuvre pour montrer que tel ensemble est ouvert ou fermé.
- Savoir justifier qu’une application donnée est continue : théorème d’opération, continuité des formes coordonnées, et donc des fonctions polynomiales ou rationnelles.
- Une fonction à valeur dans K^n est continue ssi ses composantes le sont (dém).
- Justifier la continuité de l’application A -> A¨^{-1} sur GL¨_n(K).
- Définir ce qu’est un homéomorphisme et pourquoi l’image d’un ouvert par un homéo est un ouvert.
- Montrer que x-> d(x,A) est 1 -lipschitzienne.
- Caractérisation de la continuité des applications linéaires : 5 conditions, avec dém.
- Définition de la norme d’opérateur (trois formules équivalentes).
- Calcul pratique de cette norme sur des exemples (cf. ex CCINP 37).
- Montrer que la norme infinie sur l’espace des fonctions bornées est bien une norme (on sera très précis pour les arguments sur les sup.)
- définir ce qu’est une norme d’algèbre, en donner des exemples dans l’algèbre des fonctions bornées, et dans l’algèbre des matrices carrées.
- Théorème pour les produits de limites de suites dans une algèbre normée.
- Justifier que dans un evn de dim. finie, la convergence d’une suite se vérifie « coordonnée par coordonnée ».
- Justifier que dans un evn de dim. finie, une série absolument convergente est convergente.
- Justification de l’existence de l’exp. matricielle.
- Montrer qu’une boule ouverte est ouverte, une boule fermée est fermée.
- Montrer que l’intérieur d’une boule fermée est la boule ouverte
- Montrer que l’adhérence d’une boule ouverte est la boule fermée
- Montrer qu’un s.e.v. strict est d’intérieur vide.
- Caractérisation séquentielle des points adhérence.
- Lien complémentaire de l’adhérence/intérieur du complémentaire..
- Trigonalisation : démonstration par récurrence du théorème qui dit qu’un endomorphisme ayant polynôme annulateur scindé est tz.
- Caractérisations des nilpotents en termes de v.p. dans C et autre (des équivalences très simples !)
- Les élèves doivent savoir conduire la trigonalisation concrète d’une matrice 2x 2, et d’une matrice 3 x 3 et même la réduction sous forme de Jordan dans ces cas particuliers (deux cas en dim. 3…)
- Théorème de décomposition sur les s.e.v. caractéristiques : donne une tz précisée.
- Calcul du polynôme caractéristique d’une matrice compagnon.
- Justifier que la multiplicité géométrique d’une v.p. est inférieure ou égale à sa multiplicité algébrique.
- Révisions sur les formules de changement de base, pour les vecteurs et les applications linéaires.
- valeurs propres, vecteurs propres : recherche à l’aide de l’équation aux valeurs propres sur des exemples en dim. finie ou infinie
- caractérisation : lambda v.p. d’une matrice A ssi det(A-lambda I)=0, application aux v.p. des matrices triangulaires
- Démonstration(s) du fait que des s.e.v. propres associés à des v.p. distinctes sont en somme directe
- Si lambda est v.p. d’un endomorphisme L et si P est un polynôme alors P(lambda) est v.p. de P(L). Conséquence si P est annulateur de L
- Les v.p. de L sont exactement les racines du polynôme minimal de L.
- Théorème de décomposition des noyaux : démonstration pour un produit de deux polynômes. On sera spécialement attentif à la bonne compréhension des objets manipulés (P(L)(x) et pas P(L(x)) et (PQ)(L)=P(L)o Q(L) etc…)
- Savoir donner le maximum de caractérisation d’une matrice diagonalisable et la C.S. « n v.p. distinctes en dim. n « .
- Toute la Planche-R0 a été faite en classe. On pourra demander de retraiter un exercice de cette planche en question de cours.
- On pourra aussi vérifier la connaissance des théorèmes de première année : par exemple, les théorèmes sur le rang (notion dont je me suis aperçu qu’elle était mal connue) !
-
- caractérisation du rang avec les matrices extraites,
- le fait que toute matrice de rang r soit équivalente à une matrice ‘J_r’,
- ou encore qu’une matrice et sa transposée ont le même rang.
-
- Le cours de la semaine : Arithmétique/Polynôme et Polynômes appliqués à des matrices.
Question sur cours :
- savoir définir un idéal et savoir pourquoi les idéaux de K[X] sont principaux,
- savoir la prop-définition du PGCD et PPCM avec les idéaux et pourquoi cette déf entraîne immédiatement que tout multiple commun est un multiple du PPCM et tout diviseur commun est un diviseur du PGCD
- Savoir la caractérisation des éléments inversibles dans Z/nZ.
- Propriété définition du polynôme minimal d’une matrice, d’un endomorphisme.
- Connaitre le polynôme minimal d’une matrice diagonale.
- Savoir pourquoi l’inverse d’une matrice A est un polynôme en A.
- Savoir pourquoi P(A) inversible dans M_n(K) ssi P et mu_A sont premiers entre eux.
- Définition de la divergence grossière, et savoir démontrer que si la série de terme général (u_n) converge alors (u_n) tend vers zéro.
- Test de d’Alembert avec démonstration.
- Sur la comparaison série/intégrale, pour les colleurs le programme officiel a un peu changé il s’agit maintenant plus d’un savoir faire que d’un résultat, savoir justifier le D.A. de H_n à la précision o(1).
- Citer précisément le théorème de sommation des relations de comparaison et démontrer un cas.
- Citer le Théorème spécial pour certaines séries alternées avec comme conclusion aussi le signe du reste et la majoration du reste.
- Savoir mettre en oeuvre le lien suites/séries pour gagner un terme supplémentaire dans le D.A. de H_n. (précision o(1/n)).
- Révisions sur les formules de changement de base, pour les vecteurs et les applications linéaires.
- valeurs propres, vecteurs propres : recherche à l’aide de l’équation aux valeurs propres sur des exemples en dim. finie ou infinie
- caractérisation : lambda v.p. d’une matrice A ssi det(A-lambda I)=0, application aux v.p. des matrices triangulaires
- Démonstration(s) du fait que des s.e.v. propres associés à des v.p. distinctes sont en somme directe
- Si lambda est v.p. d’un endomorphisme L et si P est un polynôme alors P(lambda) est v.p. de P(L). Conséquence si P est annulateur de L
- Les v.p. de L sont exactement les racines du polynôme minimal de L.
- Théorème de décomposition des noyaux : démonstration pour un produit de deux polynômes. On sera spécialement attentif à la bonne compréhension des objets manipulés (P(L)(x) et pas P(L(x)) et (PQ)(L)=P(L)o Q(L) etc…)
- Savoir donner le maximum de caractérisation d’une matrice diagonalisable et la C.S. « n v.p. distinctes en dim. n « .
- Toute la Planche-R0 a été faite en classe. On pourra demander de retraiter un exercice de cette planche en question de cours.
- On pourra aussi vérifier la connaissance des théorèmes de première année : par exemple, les théorèmes sur le rang (notion dont je me suis aperçu qu’elle était mal connue) !
-
- caractérisation du rang avec les matrices extraites,
- le fait que toute matrice de rang r soit équivalente à une matrice ‘J_r’,
- ou encore qu’une matrice et sa transposée ont le même rang.
-
- Le cours de la semaine : Arithmétique/Polynôme et Polynômes appliqués à des matrices.
Question sur cours :
- savoir définir un idéal et savoir pourquoi les idéaux de K[X] sont principaux,
- savoir la prop-définition du PGCD et PPCM avec les idéaux et pourquoi cette déf entraîne immédiatement que tout multiple commun est un multiple du PPCM et tout diviseur commun est un diviseur du PGCD
- Savoir la caractérisation des éléments inversibles dans Z/nZ.
- Propriété définition du polynôme minimal d’une matrice, d’un endomorphisme.
- Connaitre le polynôme minimal d’une matrice diagonale.
- Savoir pourquoi l’inverse d’une matrice A est un polynôme en A.
- Savoir pourquoi P(A) inversible dans M_n(K) ssi P et mu_A sont premiers entre eux.
- Définition de la divergence grossière, et savoir démontrer que si la série de terme général (u_n) converge alors (u_n) tend vers zéro.
- Test de d’Alembert avec démonstration.
- Sur la comparaison série/intégrale, pour les colleurs le programme officiel a un peu changé il s’agit maintenant plus d’un savoir faire que d’un résultat, savoir justifier le D.A. de H_n à la précision o(1).
- Citer précisément le théorème de sommation des relations de comparaison et démontrer un cas.
- Citer le Théorème spécial pour certaines séries alternées avec comme conclusion aussi le signe du reste et la majoration du reste.
- Savoir mettre en oeuvre le lien suites/séries pour gagner un terme supplémentaire dans le D.A. de H_n. (précision o(1/n)).
- ouverts et fermés relatifs : définition d’un ouvert de A, d’un fermé de A, caractérisations (démo non exigibles).
- déf. de la continuité en un point et caractérisation avec les voisinages avec démonstration.
- caractérisation globale de la continuité : f est continue de A dans F ssi la préimage d’un ouvert de F est un ouvert de A (resp. d’un fermé) : démo. non exigible, par contre : savoir bien la mettre en oeuvre pour montrer que tel ensemble est ouvert ou fermé.
- Savoir justifier qu’une application donnée est continue : théorème d’opération, continuité des formes coordonnées, et donc des fonctions polynomiales ou rationnelles.
- Une fonction à valeur dans K^n est continue ssi ses composantes le sont (dém).
- Justifier la continuité de l’application A -> A¨^{-1} sur GL¨_n(K).
- Définir ce qu’est un homéomorphisme et pourquoi l’image d’un ouvert par un homéo est un ouvert.
- Montrer que x-> d(x,A) est 1 -lipschitzienne.
- Caractérisation de la continuité des applications linéaires : 5 conditions, avec dém.
- Définition de la norme d’opérateur (trois formules équivalentes).
- Calcul pratique de cette norme sur des exemples (cf. ex CCINP 37).
- Montrer que la norme infinie sur l’espace des fonctions bornées est bien une norme (on sera très précis pour les arguments sur les sup.)
- définir ce qu’est une norme d’algèbre, en donner des exemples dans l’algèbre des fonctions bornées, et dans l’algèbre des matrices carrées.
- Théorème pour les produits de limites de suites dans une algèbre normée.
- Justifier que dans un evn de dim. finie, la convergence d’une suite se vérifie « coordonnée par coordonnée ».
- Justifier que dans un evn de dim. finie, une série absolument convergente est convergente.
- Justification de l’existence de l’exp. matricielle.
- Montrer qu’une boule ouverte est ouverte, une boule fermée est fermée.
- Montrer que l’intérieur d’une boule fermée est la boule ouverte
- Montrer que l’adhérence d’une boule ouverte est la boule fermée
- Montrer qu’un s.e.v. strict est d’intérieur vide.
- Caractérisation séquentielle des points adhérence.
- Lien complémentaire de l’adhérence/intérieur du complémentaire..
- Trigonalisation : démonstration par récurrence du théorème qui dit qu’un endomorphisme ayant polynôme annulateur scindé est tz.
- Caractérisations des nilpotents en termes de v.p. dans C et autre (des équivalences très simples !)
- Les élèves doivent savoir conduire la trigonalisation concrète d’une matrice 2x 2, et d’une matrice 3 x 3 et même la réduction sous forme de Jordan dans ces cas particuliers (deux cas en dim. 3…)
- Théorème de décomposition sur les s.e.v. caractéristiques : donne une tz précisée.
- Calcul du polynôme caractéristique d’une matrice compagnon.
- Justifier que la multiplicité géométrique d’une v.p. est inférieure ou égale à sa multiplicité algébrique.
- Révisions sur les formules de changement de base, pour les vecteurs et les applications linéaires.
- valeurs propres, vecteurs propres : recherche à l’aide de l’équation aux valeurs propres sur des exemples en dim. finie ou infinie
- caractérisation : lambda v.p. d’une matrice A ssi det(A-lambda I)=0, application aux v.p. des matrices triangulaires
- Démonstration(s) du fait que des s.e.v. propres associés à des v.p. distinctes sont en somme directe
- Si lambda est v.p. d’un endomorphisme L et si P est un polynôme alors P(lambda) est v.p. de P(L). Conséquence si P est annulateur de L
- Les v.p. de L sont exactement les racines du polynôme minimal de L.
- Théorème de décomposition des noyaux : démonstration pour un produit de deux polynômes. On sera spécialement attentif à la bonne compréhension des objets manipulés (P(L)(x) et pas P(L(x)) et (PQ)(L)=P(L)o Q(L) etc…)
- Savoir donner le maximum de caractérisation d’une matrice diagonalisable et la C.S. « n v.p. distinctes en dim. n « .
- Toute la Planche-R0 a été faite en classe. On pourra demander de retraiter un exercice de cette planche en question de cours.
- On pourra aussi vérifier la connaissance des théorèmes de première année : par exemple, les théorèmes sur le rang (notion dont je me suis aperçu qu’elle était mal connue) !
-
- caractérisation du rang avec les matrices extraites,
- le fait que toute matrice de rang r soit équivalente à une matrice ‘J_r’,
- ou encore qu’une matrice et sa transposée ont le même rang.
-
- Le cours de la semaine : Arithmétique/Polynôme et Polynômes appliqués à des matrices.
Question sur cours :
- savoir définir un idéal et savoir pourquoi les idéaux de K[X] sont principaux,
- savoir la prop-définition du PGCD et PPCM avec les idéaux et pourquoi cette déf entraîne immédiatement que tout multiple commun est un multiple du PPCM et tout diviseur commun est un diviseur du PGCD
- Savoir la caractérisation des éléments inversibles dans Z/nZ.
- Propriété définition du polynôme minimal d’une matrice, d’un endomorphisme.
- Connaitre le polynôme minimal d’une matrice diagonale.
- Savoir pourquoi l’inverse d’une matrice A est un polynôme en A.
- Savoir pourquoi P(A) inversible dans M_n(K) ssi P et mu_A sont premiers entre eux.
- Définition de la divergence grossière, et savoir démontrer que si la série de terme général (u_n) converge alors (u_n) tend vers zéro.
- Test de d’Alembert avec démonstration.
- Sur la comparaison série/intégrale, pour les colleurs le programme officiel a un peu changé il s’agit maintenant plus d’un savoir faire que d’un résultat, savoir justifier le D.A. de H_n à la précision o(1).
- Citer précisément le théorème de sommation des relations de comparaison et démontrer un cas.
- Citer le Théorème spécial pour certaines séries alternées avec comme conclusion aussi le signe du reste et la majoration du reste.
- Savoir mettre en oeuvre le lien suites/séries pour gagner un terme supplémentaire dans le D.A. de H_n. (précision o(1/n)).
- Révisions sur les formules de changement de base, pour les vecteurs et les applications linéaires.
- valeurs propres, vecteurs propres : recherche à l’aide de l’équation aux valeurs propres sur des exemples en dim. finie ou infinie
- caractérisation : lambda v.p. d’une matrice A ssi det(A-lambda I)=0, application aux v.p. des matrices triangulaires
- Démonstration(s) du fait que des s.e.v. propres associés à des v.p. distinctes sont en somme directe
- Si lambda est v.p. d’un endomorphisme L et si P est un polynôme alors P(lambda) est v.p. de P(L). Conséquence si P est annulateur de L
- Les v.p. de L sont exactement les racines du polynôme minimal de L.
- Théorème de décomposition des noyaux : démonstration pour un produit de deux polynômes. On sera spécialement attentif à la bonne compréhension des objets manipulés (P(L)(x) et pas P(L(x)) et (PQ)(L)=P(L)o Q(L) etc…)
- Savoir donner le maximum de caractérisation d’une matrice diagonalisable et la C.S. « n v.p. distinctes en dim. n « .
- Toute la Planche-R0 a été faite en classe. On pourra demander de retraiter un exercice de cette planche en question de cours.
- On pourra aussi vérifier la connaissance des théorèmes de première année : par exemple, les théorèmes sur le rang (notion dont je me suis aperçu qu’elle était mal connue) !
-
- caractérisation du rang avec les matrices extraites,
- le fait que toute matrice de rang r soit équivalente à une matrice ‘J_r’,
- ou encore qu’une matrice et sa transposée ont le même rang.
-
- Le cours de la semaine : Arithmétique/Polynôme et Polynômes appliqués à des matrices.
Question sur cours :
- savoir définir un idéal et savoir pourquoi les idéaux de K[X] sont principaux,
- savoir la prop-définition du PGCD et PPCM avec les idéaux et pourquoi cette déf entraîne immédiatement que tout multiple commun est un multiple du PPCM et tout diviseur commun est un diviseur du PGCD
- Savoir la caractérisation des éléments inversibles dans Z/nZ.
- Propriété définition du polynôme minimal d’une matrice, d’un endomorphisme.
- Connaitre le polynôme minimal d’une matrice diagonale.
- Savoir pourquoi l’inverse d’une matrice A est un polynôme en A.
- Savoir pourquoi P(A) inversible dans M_n(K) ssi P et mu_A sont premiers entre eux.
- Définition de la divergence grossière, et savoir démontrer que si la série de terme général (u_n) converge alors (u_n) tend vers zéro.
- Test de d’Alembert avec démonstration.
- Sur la comparaison série/intégrale, pour les colleurs le programme officiel a un peu changé il s’agit maintenant plus d’un savoir faire que d’un résultat, savoir justifier le D.A. de H_n à la précision o(1).
- Citer précisément le théorème de sommation des relations de comparaison et démontrer un cas.
- Citer le Théorème spécial pour certaines séries alternées avec comme conclusion aussi le signe du reste et la majoration du reste.
- Savoir mettre en oeuvre le lien suites/séries pour gagner un terme supplémentaire dans le D.A. de H_n. (précision o(1/n)).
- Révisions sur les formules de changement de base, pour les vecteurs et les applications linéaires.
- valeurs propres, vecteurs propres : recherche à l’aide de l’équation aux valeurs propres sur des exemples en dim. finie ou infinie
- caractérisation : lambda v.p. d’une matrice A ssi det(A-lambda I)=0, application aux v.p. des matrices de petites tailles et des matrices triangulaires
- Démonstration du fait que des s.e.v. propres associés à des v.p. distinctes sont en somme directe
- Si lambda est v.p. d’un endomorphisme L et si P est un polynôme alors P(lambda) est v.p. de P(L). Conséquence si P est annulateur de L, Sp(L) est inclus dans Z(P).
- Les v.p. de L sont exactement les racines du polynôme minimal de L.
- Théorème de décomposition des noyaux : démonstration pour un produit de deux polynômes. On sera spécialement attentif à la bonne compréhension des objets manipulés (P(L)(x) et pas P(L(x)) et (PQ)(L)=P(L)o Q(L) etc…)
- Savoir donner le maximum de caractérisations d’une matrice diagonalisable et la C.S. « n v.p. distinctes en dim. n » mais en fait retenir surtout et pour chaque exercice qu’il y a d »un côté le point de vue géométrique (avec les vecteurs propres et les ses propres) et le point de vue algébrique (avec les polynômes annulateurs, le minimal;
- Qu’est-ce qu’un anneau, qu’est-ce corps ? Montrer que Z/nZ est un corps ssi Z/nZ est intègre ssi n est un nombre premier.
- Plus généralement : pour a dans Z, montrer que la classe de a est inversible dans l’anneau Z/nZ ssi a et n sont premiers entre eux
- savoir définir ce qu’est un idéal et savoir la forme des idéaux de K[X] et de Z (dém. sur K[X]).
- Définir le polynôme minimal d’un matrice (resp. d’un endomorphisme d’un e.v. de dim. finie) et savoir pourquoi tout polynôme annulateur est divisible par le polynôme minimal.
- Expliciter le polynôme minimal d’une matrice diagonale.
- Montrer que dim K[A]=deg(mu_A).
- Montrer que si A est une matrice inversible alors A^{-1} est dans K[A].
- Montrer que si A est une matrice et P est un polynôme alors P(A) est une matrice inversible ssi P est premier avec le polynôme minimal de A.
- Somme directe de plusieurs s.e.v.: définitions, différentes caractérisations
- Matrices par blocs : produits, opérations élémentaires sur les blocs, formule du déterminant d’une matrice triangulaire par bloc (deux démonstrations).
- Définition de la divergence grossière, et savoir démontrer que si la série de terme général (u_n) converge alors (u_n) tend vers zéro.
- Test de d’Alembert avec démonstration.
- Sur la comparaison série/intégrale, pour les colleurs le programme officiel a un peu changé il s’agit maintenant plus d’un savoir faire que d’un résultat, savoir justifier le D.A. de H_n à la précision o(1).
- Citer précisément le théorème de sommation des relations de comparaison et démontrer un cas.
- Citer le Théorème spécial pour certaines séries alternées avec comme conclusion aussi le signe du reste et la majoration du reste.
- Savoir mettre en oeuvre le lien suites/séries pour gagner un terme supplémentaire dans le D.A. de H_n. (précision o(1/n)) ou donner l’idée de la preuve de la formule de Stirling et en faire une ou deux étapes.
- Révisions sur les suites récurrentes u_{n+1}=f(u_n) ou les suites définies
- Familles sommables : savoir bien distinguer entre le cas positifs et le cas à signe variable/complexe. Savoir bien mettre en oeuvre le théorème de sommation terme par paquets sans justification particulière que la positivité dans le cas positif, et au contraire avec justification préalable de la sommabilité dans le cas général.. justement avec le T.S.P. positif.
Banque CCINP ex 1 à 20 et 59 à 76. (Ne tardez pas à réviser ces exercices CCINP vous devez les connaître sur les bouts des doigts).
Pour la semaine du 30 mai au 2 juin : ex 1 à 25 et 50 à 83.
Pour la semaine du 5 juin au 10 juin : ex 1 à 45 et 50 à 94.
A partir du 12 juin : toute la banque.
Semaine 23 : du lundi 27 mars
Attention : dernière semaine de colles avant les écrits.
Thème : calcul différentiel, révision du programme précédent et les rajouts qui suivent. Par ailleurs, on peut aussi poser des questions de révisions sur les endomorphismes d’un espace euclidien.
Calcul diff. on rajoute :
-
- Exemple de recherches d’extrema sous-contrainte i.e. pour f_X
- théorème dans le cas où X est une hypersurface.
- études pratiques dans le cas où on peut paramétrer X
- Calcul différentiel d’ordre 2 :
- fonctions C^2, C^k, théorème de Schwarz (admis)
- Calcul de la dérivée seconde de t->f(a+tx)
- Définition de la Hessienne d’une fonction f : U -> R, expliquer pourquoi c’est aussi la jacobienne du gradient de f.
- Savoir citer le théorème de Taylor-Young à l’ordre 2 (admis)
- C.N. de min. local : point critique a tel que Hf(a) soit symétrique positive (savoir dém).
- C.S. de min. local : point critique a tel que Hf(a) soit définie positive. (savoir dém.)
- Pratique en dim. 2 avec det(Hf(a)) et Tr(Hf(a)).
- Exemple où Hf(a) est dégénérée (0 v.p.) en exercice.
- E.D.P. d’ordre 1 et 2 :
- savoir justement proprement la « primitivation par rapport à une variable » (convexité par rapport à la variable).
- Exemples de résolution par changement de variable.
- Tous les exercices de la Banque CCINP cité en haut de planche.
- Toutes les exercices de la planche de 1 à 18 auront été traités, (peut-être plus), la suite lundi.
- Exemple de recherches d’extrema sous-contrainte i.e. pour f_X
- Planche-F2
-
- Définition de la dérivée D_v f(a) de la fonction f selon le vecteur v au point a et lien avec les dérivées partielles, cas où f est une norme N et a=0 ?
- Savoir qu’il existe des fonctions f telles que D_v f(a) existe pour tout v et qui ne sont pourtant pas continue en a (exemple sur la planche ou en cours).
- Définition de la différentiabilité : existence d’un D.L. 1, définition du gradient pour les fonctions à valeurs scalaires.
- Faire BEAUCOUP de calculs de différentielle (de gradient) avec des D.L. 1 comme ceux de la planche ex 5,6,7.
- Déf. des fonctions de classe C^1 : l’application x-> df(x) est continue, mais surtout caractérisation miraculeuse avec les dérivées partielles
- Exercices concrets où l’on utilise le point précédent (cf. planche et banque CCINP).
- Formule sur la différentielle d’une composée d(f o g)=, deux cas particuliers très utiles si l’espace intermédiaire est R et surtout si l’espace de départ est R (dérivée selon une courbe à savoir par coeur !)
- Formule d’intégration le long d’un chemin. Application si df=0 sur un ouvert c.p.a. alors f est constante.
- C.N. d’extremum local en un point d’un ouvert : point critique.
- Vecteur tangent en un point x à un sous-ensemble Xde R^n : définition, exemples, structure de cône de l’ensemble T_x X de ces vecteurs.
- Exemple si X est une sphère (savoir refaire) dans R^n.
- Cas général d’un point régulier x d’une hypersurface g=0 : T_x X=ker dg(x).
- Trois définitions équivalentes de la dérivabilité pour f : I -> E (dém. non demandée)
- Dérivée de L o f si f est dérivable de I dans E et L est linéaire de E dans F (dém.)
- Dérivée de B(f,g) si f (resp. g) sont dérivables de I dans E (resp. dans F) et B : E x F-> G est bilinéaire
- Extension du point précédent aux applications n-linéaires (typiquement déterminant).
- T.A.F. généralisé à deux fonctions » f'(c) (g(b)-g(a))=g'(c)(f(b)-f(a)) » démonstration vectorielle
- Dérivation de t-> exp(tA) par théorème de dérivation terme à terme à valeurs vectorielles
- Inégalité triangulaire pour les intégrales de fonctions vectorielles et application à l’I.A.F. dans l’hypothèse C^1.
- Formules de Taylor à savoir parfaitement.
- Moments d’ordre r d’une v.a.d. : si X admet un moment d’ordre r alors X admet un moment d’ordre s pour tout s<r.
- Calculs des variances des lois usuelles et notamment géométriques et Poisson et cas de loi binomiale comme sommes de v.a. indépendantes
- Covariance, application à la variance d’une somme
- Deux inégalités de Cauchy-Schwarz dans le contexte probabiliste, l’une avec la Covariance, l’une avec (X,Y)->E(XY)
- Série et fonction génératrice : deux définitions. La série génératrice détermine la loi
- Fonction génératrice d’une somme de v.a.d. indépendantes application à la loi binomiale, à la somme de deux v.a. de Poisson indépendantes
- Calcul de l’espérance (resp. de E(X^2)) en dérivant la fonction génératrice
- Inégalité de Markov et de Tchebychev, application méthode du 1er moment ou 2ème moment pour l’étude de P(X=0).
- Loi faible des grands nombres: énoncé et démonstration.
- Définir ce qu’est une tribu et exemples simples sur la planche P1.
- Qu’est-ce qu’une probabilité ? Démontrer la propriété de continuité croissante.
- Démontrer la sous-additivité dénombrable des probabilités.
- Donner des propriétés de l’espace probabilisé décrivant le jeu à pile ou face infini (où l’existence de la proba est bien sûr admise) : quelle tribu, comment montrer que la probabilité des singletons est nulle.
- Dans l’exemple précédent donner un exemple de système quasi-complet d’événements (qui n’est pas « complet »).
- Evénement « A_n est réalisé infiniment souvent » décrit avec inter et union, premier lemme de Borel-Cantelli (exercice Planche-P1)
- Définition d’une v.a.d. : savoir vérifier les conditions de la déf. d’une v.a.d : exemple du temps d’attente de succès dans une suite de tirages de Bernoulli (v.a.d. de loi géométrique).
- Caractérisation des v.a. géométriques par le caractère « sans-mémoire »
- Convergence en loi de v.a. suivant B(n,lambda/n) vers P(lambda)
- Indépendance des v.a.d. : déf. équivalentes (dém. non demandée).
- Espérance des v.a. géométriques et de Poisson.
- Propriété de l’espérance : formule de transfert, linéarité.
- Calcul de l’espérance à l’aide des P¨(X>x).
- Pour f autoadjoint, définir la forme bilinéaire symétrique associée à f (à savoir (x,y)-> (f(x)|y)), et la forme quadratique associée x->(f(x)|x). Chacun de ces trois objets détermine les autres : pourquoi ? (Formule de polarisation).
- Démontrer qu’un endomorphisme autoadjoint admet au moins une valeur propre (en se ramenant à la dim. 2).
- En admettant le résultat précédent, démontrer le théorème spectral pour les autoadjoints.
- Ecriture de la forme quadratique (mot H.P.) x-> (f(x)|x) dans une b.o.n. de dz. de f, application à une caractérisation de la plus grande et de la plus petite v.p. de f.
- Définition des autoadjoints positifs (resp. matrices symétriques positives) et caractérisation par le spectre.
- Déf. des autoadjoints définis positifs, caractérisation par le spectre, lien avec la notion de produit scalaire.
- Tous les exercices de la planche ont été traités sauf le 17 : Planche-R4
- Les exercices 10, 11, 12 de la Planche-R2
- Les exercices 4 à 8 et l’ex. 11 de la Planche-R3
- Ne pas négliger les calculs concrets : banque CCINP Ex. 68, et toujours des projections orthogonales (décidément mal comprises) CCINP Ex. 81,82, et des calculs de matrices de projections…
- Définition de l’adjoint d’un endomorphisme et prop. de l’application u-> u*
- Si F est un s.e.v. stable par u, alors l’orthogonal de F est stable par u*
- La matrice de u* dans une b.o.n. est la transposée de celle de u
- Déf. des isométries vectorielles et caractérisation par la conservation du produit scalaire et par f*=f^{-1}
- Caractérisation matricielle des isométries vectorielles et déf. des matrices orthogonale.
- Déterminant d’une matrice orthogonale. Donner une matrice de déterminant 1 non orthogonale.
- Une matrice orthogonale symétrique est une matrice de symétrie orthogonale.
- Thme de classification des matrices dans O_2(R).
- Thme de classification de toutes les isométries vectorielles : énoncé, étapes de la preuve.
- Citer le théorème d’approximation uniforme des fonctions c.p.m. par des fonctions en escalier et savoir l’appliquer pour démontrer le théorème de Riemann-Lebesgue sur un segment (thme H.P. mais à connaître aussi bien pour le résultat que pour la méthode).
- Citer le théorème d’approximation de Weierstrass et montrer qu’on ne peut pas espérer une CVU sur R entier car si une suite de polynômes CVU sur R entier….
- Savoir refaire la Q3 et le « lemme de Dirac » du TD : TD-Chap-T4-convolution-Weierstrass
- Espaces préhilbertiens : montrer que le produit scalaire (p.s.) est une forme bilinéaire continue.
- Exercice : lemme des moments :
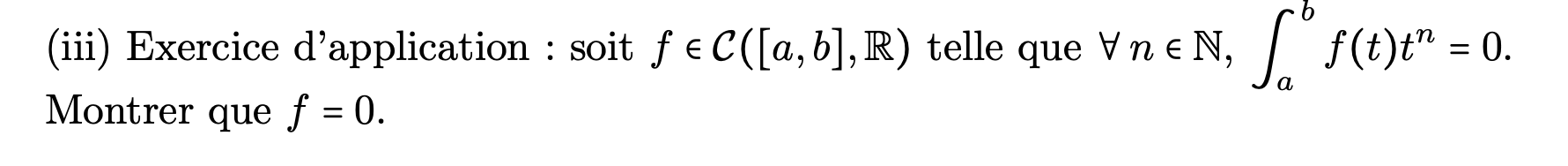
- Savoir montrer:

- Donner des exemples de sev stricts denses dans deux espaces préhilbertiens différents.
- Calcul pratique de l’orthogonalisation de Gram-Schmidt : par exemple de (1,X,X^2) pour un p.s. intégrale.
- Formule du projeté orthogonal sur F si on a une base orthogonale de F : calculs concrets.
- Théorème de meilleure approximation par le projeté orthogonal, dém (Pythagore)
- Applications concretes de ce théorème de meilleure approximation pour la minimisation d’une intégrale…. et dans le cadre matriciel cf. Banque CCINP ex. 80, 81 et 82.
- Exercice de la Planche-T4: seuls les ex. 4,5,6,7 sont « exigibles ».
- Montrer le théorème de Bolzano-Weierstrass (B.W.) dans C en admettant le résultat dans R.
- Montrer qu’un compact de E est fermé borné dans E.
- Montrer qu’un fermé dans un compact est compact.
- Donner un exemple de fermé borné non compact (aussi exercice 13 banque CCINP sur ce sujet mais penser au cadre préhilbertien aussi).
- Montrer que l’image continue d’un compact est compacte.
- Théorème des bornes atteintes pour les fonctions d’un compact dans R.
- B.W. en dim. finie : les compact d’un e.v.n. de dim. finie sont les fermés bornés.
- Montrer qu’un s.e.v. de dim. finie est toujours fermé dans tout e.v.n.
- Parties connexes par arc (c.p.a.) de R?
- Image continue d’un c.p.a.
- Connexité par arc pour montrer qu’une fonction d’un intervalle I de R dans R continue injective est strictement monotone.
- Montrer que tout ensemble infini contient un sous-ensemble dnb,
- Montrer que toute partie de N est finie ou dnb, et donc aussi toute partie d’un ensemble dnb est dnb
- Montrer que NxN est dnb et pourquoi le produit de deux ensembles dnb est dnb
- Pourquoi Q est-il dnb?
- Une union dnb d’ensembles dnb est dnb
- Un produit fini d’ensemble dnb est dnb (réc. immédiate non demandée) contre-exemple pour un produit infini, construction diagonale de Cantor.
- Déf du développement décimal ou dyadique propre de R, application à la non dnb.
- séries entières (quasiment toute la planche à été traitée, les élèves devraient donc bénéficier de plus de recul sur le sujet) : privilégier déjà les aspects calculatoires quasi « algébriques » (calculs de D.S.E., E.D., D.E.S) cf. ex. 8 à 15 de la planche S3, et pour les plus avancé.e.s. on pourra aborder les questions d’analyse plus fine (ex. 16 et suivants pl. S3).
- intégrales à paramètres : là rester simple car la pratique doit encore s’affermir, seul les 5 premiers exercices de la planche I3 sont exigibles (le 4 et 5 devant être finis pendant les vacances). Ces intégrales à paramètres reviendront sûrement pour les colles de la semaine suivante.
- Lemme d’Abel, dém. et (prop.-)-définition du rayon de convergence.
- Lemme de d’Alembert pour les séries entières : dém. avec le lemme pour les séries numériques.
- Prop. ;
 ont même rayon de convergence (au programme officiel pour alpha=1, démontrée, pour pas plus cher pour alpha qcq donc je pense qu’on peut s’en servir pour alpha quelconque).
ont même rayon de convergence (au programme officiel pour alpha=1, démontrée, pour pas plus cher pour alpha qcq donc je pense qu’on peut s’en servir pour alpha quelconque). - Rayon de convergence d’une somme et produit de Cauchy.
- Continuité de la fonction somme dans le disque ouvert de convergence.
- Pour ce qui la variable est réelle :
- Théorème de continuité radiale d’Abel : énoncé seulement, mais savoir l’appliquer sur des exemples (série harmonique alternée…)
- Dérivation terme à terme automatique pour les sommes de séries entières
- unicité des coefficients du D.S.E., série de Taylor, rigidité des fonctions D.S.E.
- DSE des fonctions usuelles : preuve de la formule du binôme (1+x)^a pour a réel avec la méthode de l’E.D.
- Banque CCINP cf haut de la planche.
- Exercice : Montrer que si I est BORNE et (f_n) est une suite de fonctions L^1 sur I qui CVU sur I vers une fonction f c.p.m. alors f est L^1 et la suite des intégrales des (f_n) CV vers celle de f (généralisation du théorème connu sur les segments au cas borné).
- Donner un exemple où le résultat précédent n’est PAS vrai avec I un intervalle non borné. Expliquer le problème.
- Application du T.C.D. avec des « bornes variables »:

- Etude des intégrales de Wallis : détermination d’un équivalent
- Méthode l’I.P.P fait sortir le terme prépondérant pour un équivalent de :
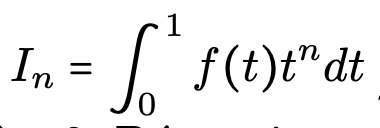
- Le même équivalent par la méthode de changement de variable.
- Intégration terme à terme d’une CVU sur un segment :
-
- application aux séries entières : montrer que :
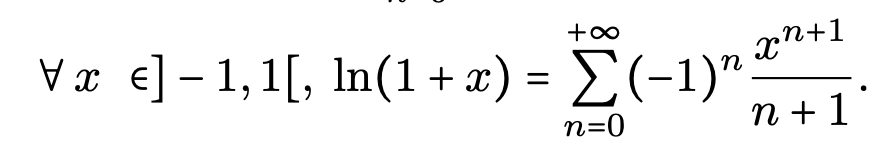
- applications aux séries trigonométriques (très important car H.P. mais dans tellement de sujets d’écrits de maths et dans le cours de physique)

- application aux séries entières : montrer que :
-
- Théorème d’intégration terme à terme de Lebesgue en deux théorèmes : cas positif et cas signe quelconque. Exemple du second cas :

- Ce qu’on fait quand le théorème ne s’applique pas. Exemple :

- Planche I2 : les exercices 1 à 4 ainsi que le 6 ont été faits en classe cette semaine. D’autres seront corrigés lundi. Planche-I2
- On pourra demander un énoncé précis de théorème en début de colle.
- Démonstration du théorème de continuité d’une limite uniforme d’une suite de fonction continue.
- Démonstration du théorème d’intégration d’une limite uniforme sur un segment.
- Le théorème d’interversion des limites a été admis.
- Exemple de la fonction zeta réelle : caractère C infini, limite à l’infini
- Exemple de la suite de fonctions x-> n sin(x/n) méthode pour la CVU sur les segments et pourquoi on n’ a pas CVU sur R
- Méthode d’encadrement par des intégrales pour un équivalent quand x->0 de la somme des exp(-x sqrt(n)).
- ouverts et fermés relatifs : définition d’un ouvert de A, d’un fermé de A, caractérisations (démo non exigibles).
- déf. de la continuité en un point et caractérisation avec les voisinages avec démonstration.
- caractérisation globale de la continuité : f est continue de A dans F ssi la préimage d’un ouvert de F est un ouvert de A (resp. d’un fermé) : démo. non exigible, par contre : savoir bien la mettre en oeuvre pour montrer que tel ensemble est ouvert ou fermé.
- Savoir justifier qu’une application donnée est continue : théorème d’opération, continuité des formes coordonnées, et donc des fonctions polynomiales ou rationnelles.
- Une fonction à valeur dans K^n est continue ssi ses composantes le sont (dém).
- Justifier la continuité de l’application A -> A¨^{-1} sur GL¨_n(K).
- Définir ce qu’est un homéomorphisme et pourquoi l’image d’un ouvert par un homéo est un ouvert.
- Montrer que x-> d(x,A) est 1 -lipschitzienne.
- Caractérisation de la continuité des applications linéaires : 5 conditions, avec dém.
- Définition de la norme d’opérateur (trois formules équivalentes).
- Calcul pratique de cette norme sur des exemples (cf. ex CCINP 37).
- Montrer que la norme infinie sur l’espace des fonctions bornées est bien une norme (on sera très précis pour les arguments sur les sup.)
- définir ce qu’est une norme d’algèbre, en donner des exemples dans l’algèbre des fonctions bornées, et dans l’algèbre des matrices carrées.
- Théorème pour les produits de limites de suites dans une algèbre normée.
- Justifier que dans un evn de dim. finie, la convergence d’une suite se vérifie « coordonnée par coordonnée ».
- Justifier que dans un evn de dim. finie, une série absolument convergente est convergente.
- Justification de l’existence de l’exp. matricielle.
- Montrer qu’une boule ouverte est ouverte, une boule fermée est fermée.
- Montrer que l’intérieur d’une boule fermée est la boule ouverte
- Montrer que l’adhérence d’une boule ouverte est la boule fermée
- Montrer qu’un s.e.v. strict est d’intérieur vide.
- Caractérisation séquentielle des points adhérence.
- Lien complémentaire de l’adhérence/intérieur du complémentaire..
- Trigonalisation : démonstration par récurrence du théorème qui dit qu’un endomorphisme ayant polynôme annulateur scindé est tz.
- Caractérisations des nilpotents en termes de v.p. dans C et autre (des équivalences très simples !)
- Les élèves doivent savoir conduire la trigonalisation concrète d’une matrice 2x 2, et d’une matrice 3 x 3 et même la réduction sous forme de Jordan dans ces cas particuliers (deux cas en dim. 3…)
- Théorème de décomposition sur les s.e.v. caractéristiques : donne une tz précisée.
- Calcul du polynôme caractéristique d’une matrice compagnon.
- Justifier que la multiplicité géométrique d’une v.p. est inférieure ou égale à sa multiplicité algébrique.
- Révisions sur les formules de changement de base, pour les vecteurs et les applications linéaires.
- valeurs propres, vecteurs propres : recherche à l’aide de l’équation aux valeurs propres sur des exemples en dim. finie ou infinie
- caractérisation : lambda v.p. d’une matrice A ssi det(A-lambda I)=0, application aux v.p. des matrices triangulaires
- Démonstration(s) du fait que des s.e.v. propres associés à des v.p. distinctes sont en somme directe
- Si lambda est v.p. d’un endomorphisme L et si P est un polynôme alors P(lambda) est v.p. de P(L). Conséquence si P est annulateur de L
- Les v.p. de L sont exactement les racines du polynôme minimal de L.
- Théorème de décomposition des noyaux : démonstration pour un produit de deux polynômes. On sera spécialement attentif à la bonne compréhension des objets manipulés (P(L)(x) et pas P(L(x)) et (PQ)(L)=P(L)o Q(L) etc…)
- Savoir donner le maximum de caractérisation d’une matrice diagonalisable et la C.S. « n v.p. distinctes en dim. n « .
- Toute la Planche-R0 a été faite en classe. On pourra demander de retraiter un exercice de cette planche en question de cours.
- On pourra aussi vérifier la connaissance des théorèmes de première année : par exemple, les théorèmes sur le rang (notion dont je me suis aperçu qu’elle était mal connue) !
-
- caractérisation du rang avec les matrices extraites,
- le fait que toute matrice de rang r soit équivalente à une matrice ‘J_r’,
- ou encore qu’une matrice et sa transposée ont le même rang.
-
- Le cours de la semaine : Arithmétique/Polynôme et Polynômes appliqués à des matrices.
Question sur cours :
- savoir définir un idéal et savoir pourquoi les idéaux de K[X] sont principaux,
- savoir la prop-définition du PGCD et PPCM avec les idéaux et pourquoi cette déf entraîne immédiatement que tout multiple commun est un multiple du PPCM et tout diviseur commun est un diviseur du PGCD
- Savoir la caractérisation des éléments inversibles dans Z/nZ.
- Propriété définition du polynôme minimal d’une matrice, d’un endomorphisme.
- Connaitre le polynôme minimal d’une matrice diagonale.
- Savoir pourquoi l’inverse d’une matrice A est un polynôme en A.
- Savoir pourquoi P(A) inversible dans M_n(K) ssi P et mu_A sont premiers entre eux.
- Définition de la divergence grossière, et savoir démontrer que si la série de terme général (u_n) converge alors (u_n) tend vers zéro.
- Test de d’Alembert avec démonstration.
- Sur la comparaison série/intégrale, pour les colleurs le programme officiel a un peu changé il s’agit maintenant plus d’un savoir faire que d’un résultat, savoir justifier le D.A. de H_n à la précision o(1).
- Citer précisément le théorème de sommation des relations de comparaison et démontrer un cas.
- Citer le Théorème spécial pour certaines séries alternées avec comme conclusion aussi le signe du reste et la majoration du reste.
- Savoir mettre en oeuvre le lien suites/séries pour gagner un terme supplémentaire dans le D.A. de H_n. (précision o(1/n)).
- Révisions sur les formules de changement de base, pour les vecteurs et les applications linéaires.
- valeurs propres, vecteurs propres : recherche à l’aide de l’équation aux valeurs propres sur des exemples en dim. finie ou infinie
- caractérisation : lambda v.p. d’une matrice A ssi det(A-lambda I)=0, application aux v.p. des matrices triangulaires
- Démonstration(s) du fait que des s.e.v. propres associés à des v.p. distinctes sont en somme directe
- Si lambda est v.p. d’un endomorphisme L et si P est un polynôme alors P(lambda) est v.p. de P(L). Conséquence si P est annulateur de L
- Les v.p. de L sont exactement les racines du polynôme minimal de L.
- Théorème de décomposition des noyaux : démonstration pour un produit de deux polynômes. On sera spécialement attentif à la bonne compréhension des objets manipulés (P(L)(x) et pas P(L(x)) et (PQ)(L)=P(L)o Q(L) etc…)
- Savoir donner le maximum de caractérisation d’une matrice diagonalisable et la C.S. « n v.p. distinctes en dim. n « .
- Toute la Planche-R0 a été faite en classe. On pourra demander de retraiter un exercice de cette planche en question de cours.
- On pourra aussi vérifier la connaissance des théorèmes de première année : par exemple, les théorèmes sur le rang (notion dont je me suis aperçu qu’elle était mal connue) !
-
- caractérisation du rang avec les matrices extraites,
- le fait que toute matrice de rang r soit équivalente à une matrice ‘J_r’,
- ou encore qu’une matrice et sa transposée ont le même rang.
-
- Le cours de la semaine : Arithmétique/Polynôme et Polynômes appliqués à des matrices.
Question sur cours :
- savoir définir un idéal et savoir pourquoi les idéaux de K[X] sont principaux,
- savoir la prop-définition du PGCD et PPCM avec les idéaux et pourquoi cette déf entraîne immédiatement que tout multiple commun est un multiple du PPCM et tout diviseur commun est un diviseur du PGCD
- Savoir la caractérisation des éléments inversibles dans Z/nZ.
- Propriété définition du polynôme minimal d’une matrice, d’un endomorphisme.
- Connaitre le polynôme minimal d’une matrice diagonale.
- Savoir pourquoi l’inverse d’une matrice A est un polynôme en A.
- Savoir pourquoi P(A) inversible dans M_n(K) ssi P et mu_A sont premiers entre eux.
- Définition de la divergence grossière, et savoir démontrer que si la série de terme général (u_n) converge alors (u_n) tend vers zéro.
- Test de d’Alembert avec démonstration.
- Sur la comparaison série/intégrale, pour les colleurs le programme officiel a un peu changé il s’agit maintenant plus d’un savoir faire que d’un résultat, savoir justifier le D.A. de H_n à la précision o(1).
- Citer précisément le théorème de sommation des relations de comparaison et démontrer un cas.
- Citer le Théorème spécial pour certaines séries alternées avec comme conclusion aussi le signe du reste et la majoration du reste.
- Savoir mettre en oeuvre le lien suites/séries pour gagner un terme supplémentaire dans le D.A. de H_n. (précision o(1/n)).
- ouverts et fermés relatifs : définition d’un ouvert de A, d’un fermé de A, caractérisations (démo non exigibles).
- déf. de la continuité en un point et caractérisation avec les voisinages avec démonstration.
- caractérisation globale de la continuité : f est continue de A dans F ssi la préimage d’un ouvert de F est un ouvert de A (resp. d’un fermé) : démo. non exigible, par contre : savoir bien la mettre en oeuvre pour montrer que tel ensemble est ouvert ou fermé.
- Savoir justifier qu’une application donnée est continue : théorème d’opération, continuité des formes coordonnées, et donc des fonctions polynomiales ou rationnelles.
- Une fonction à valeur dans K^n est continue ssi ses composantes le sont (dém).
- Justifier la continuité de l’application A -> A¨^{-1} sur GL¨_n(K).
- Définir ce qu’est un homéomorphisme et pourquoi l’image d’un ouvert par un homéo est un ouvert.
- Montrer que x-> d(x,A) est 1 -lipschitzienne.
- Caractérisation de la continuité des applications linéaires : 5 conditions, avec dém.
- Définition de la norme d’opérateur (trois formules équivalentes).
- Calcul pratique de cette norme sur des exemples (cf. ex CCINP 37).
- Montrer que la norme infinie sur l’espace des fonctions bornées est bien une norme (on sera très précis pour les arguments sur les sup.)
- définir ce qu’est une norme d’algèbre, en donner des exemples dans l’algèbre des fonctions bornées, et dans l’algèbre des matrices carrées.
- Théorème pour les produits de limites de suites dans une algèbre normée.
- Justifier que dans un evn de dim. finie, la convergence d’une suite se vérifie « coordonnée par coordonnée ».
- Justifier que dans un evn de dim. finie, une série absolument convergente est convergente.
- Justification de l’existence de l’exp. matricielle.
- Montrer qu’une boule ouverte est ouverte, une boule fermée est fermée.
- Montrer que l’intérieur d’une boule fermée est la boule ouverte
- Montrer que l’adhérence d’une boule ouverte est la boule fermée
- Montrer qu’un s.e.v. strict est d’intérieur vide.
- Caractérisation séquentielle des points adhérence.
- Lien complémentaire de l’adhérence/intérieur du complémentaire..
- Trigonalisation : démonstration par récurrence du théorème qui dit qu’un endomorphisme ayant polynôme annulateur scindé est tz.
- Caractérisations des nilpotents en termes de v.p. dans C et autre (des équivalences très simples !)
- Les élèves doivent savoir conduire la trigonalisation concrète d’une matrice 2x 2, et d’une matrice 3 x 3 et même la réduction sous forme de Jordan dans ces cas particuliers (deux cas en dim. 3…)
- Théorème de décomposition sur les s.e.v. caractéristiques : donne une tz précisée.
- Calcul du polynôme caractéristique d’une matrice compagnon.
- Justifier que la multiplicité géométrique d’une v.p. est inférieure ou égale à sa multiplicité algébrique.
- Révisions sur les formules de changement de base, pour les vecteurs et les applications linéaires.
- valeurs propres, vecteurs propres : recherche à l’aide de l’équation aux valeurs propres sur des exemples en dim. finie ou infinie
- caractérisation : lambda v.p. d’une matrice A ssi det(A-lambda I)=0, application aux v.p. des matrices triangulaires
- Démonstration(s) du fait que des s.e.v. propres associés à des v.p. distinctes sont en somme directe
- Si lambda est v.p. d’un endomorphisme L et si P est un polynôme alors P(lambda) est v.p. de P(L). Conséquence si P est annulateur de L
- Les v.p. de L sont exactement les racines du polynôme minimal de L.
- Théorème de décomposition des noyaux : démonstration pour un produit de deux polynômes. On sera spécialement attentif à la bonne compréhension des objets manipulés (P(L)(x) et pas P(L(x)) et (PQ)(L)=P(L)o Q(L) etc…)
- Savoir donner le maximum de caractérisation d’une matrice diagonalisable et la C.S. « n v.p. distinctes en dim. n « .
- Toute la Planche-R0 a été faite en classe. On pourra demander de retraiter un exercice de cette planche en question de cours.
- On pourra aussi vérifier la connaissance des théorèmes de première année : par exemple, les théorèmes sur le rang (notion dont je me suis aperçu qu’elle était mal connue) !
-
- caractérisation du rang avec les matrices extraites,
- le fait que toute matrice de rang r soit équivalente à une matrice ‘J_r’,
- ou encore qu’une matrice et sa transposée ont le même rang.
-
- Le cours de la semaine : Arithmétique/Polynôme et Polynômes appliqués à des matrices.
Question sur cours :
- savoir définir un idéal et savoir pourquoi les idéaux de K[X] sont principaux,
- savoir la prop-définition du PGCD et PPCM avec les idéaux et pourquoi cette déf entraîne immédiatement que tout multiple commun est un multiple du PPCM et tout diviseur commun est un diviseur du PGCD
- Savoir la caractérisation des éléments inversibles dans Z/nZ.
- Propriété définition du polynôme minimal d’une matrice, d’un endomorphisme.
- Connaitre le polynôme minimal d’une matrice diagonale.
- Savoir pourquoi l’inverse d’une matrice A est un polynôme en A.
- Savoir pourquoi P(A) inversible dans M_n(K) ssi P et mu_A sont premiers entre eux.
- Définition de la divergence grossière, et savoir démontrer que si la série de terme général (u_n) converge alors (u_n) tend vers zéro.
- Test de d’Alembert avec démonstration.
- Sur la comparaison série/intégrale, pour les colleurs le programme officiel a un peu changé il s’agit maintenant plus d’un savoir faire que d’un résultat, savoir justifier le D.A. de H_n à la précision o(1).
- Citer précisément le théorème de sommation des relations de comparaison et démontrer un cas.
- Citer le Théorème spécial pour certaines séries alternées avec comme conclusion aussi le signe du reste et la majoration du reste.
- Savoir mettre en oeuvre le lien suites/séries pour gagner un terme supplémentaire dans le D.A. de H_n. (précision o(1/n)).
- Révisions sur les formules de changement de base, pour les vecteurs et les applications linéaires.
- valeurs propres, vecteurs propres : recherche à l’aide de l’équation aux valeurs propres sur des exemples en dim. finie ou infinie
- caractérisation : lambda v.p. d’une matrice A ssi det(A-lambda I)=0, application aux v.p. des matrices triangulaires
- Démonstration(s) du fait que des s.e.v. propres associés à des v.p. distinctes sont en somme directe
- Si lambda est v.p. d’un endomorphisme L et si P est un polynôme alors P(lambda) est v.p. de P(L). Conséquence si P est annulateur de L
- Les v.p. de L sont exactement les racines du polynôme minimal de L.
- Théorème de décomposition des noyaux : démonstration pour un produit de deux polynômes. On sera spécialement attentif à la bonne compréhension des objets manipulés (P(L)(x) et pas P(L(x)) et (PQ)(L)=P(L)o Q(L) etc…)
- Savoir donner le maximum de caractérisation d’une matrice diagonalisable et la C.S. « n v.p. distinctes en dim. n « .
- Toute la Planche-R0 a été faite en classe. On pourra demander de retraiter un exercice de cette planche en question de cours.
- On pourra aussi vérifier la connaissance des théorèmes de première année : par exemple, les théorèmes sur le rang (notion dont je me suis aperçu qu’elle était mal connue) !
-
- caractérisation du rang avec les matrices extraites,
- le fait que toute matrice de rang r soit équivalente à une matrice ‘J_r’,
- ou encore qu’une matrice et sa transposée ont le même rang.
-
- Le cours de la semaine : Arithmétique/Polynôme et Polynômes appliqués à des matrices.
Question sur cours :
- savoir définir un idéal et savoir pourquoi les idéaux de K[X] sont principaux,
- savoir la prop-définition du PGCD et PPCM avec les idéaux et pourquoi cette déf entraîne immédiatement que tout multiple commun est un multiple du PPCM et tout diviseur commun est un diviseur du PGCD
- Savoir la caractérisation des éléments inversibles dans Z/nZ.
- Propriété définition du polynôme minimal d’une matrice, d’un endomorphisme.
- Connaitre le polynôme minimal d’une matrice diagonale.
- Savoir pourquoi l’inverse d’une matrice A est un polynôme en A.
- Savoir pourquoi P(A) inversible dans M_n(K) ssi P et mu_A sont premiers entre eux.
- Définition de la divergence grossière, et savoir démontrer que si la série de terme général (u_n) converge alors (u_n) tend vers zéro.
- Test de d’Alembert avec démonstration.
- Sur la comparaison série/intégrale, pour les colleurs le programme officiel a un peu changé il s’agit maintenant plus d’un savoir faire que d’un résultat, savoir justifier le D.A. de H_n à la précision o(1).
- Citer précisément le théorème de sommation des relations de comparaison et démontrer un cas.
- Citer le Théorème spécial pour certaines séries alternées avec comme conclusion aussi le signe du reste et la majoration du reste.
- Savoir mettre en oeuvre le lien suites/séries pour gagner un terme supplémentaire dans le D.A. de H_n. (précision o(1/n)).