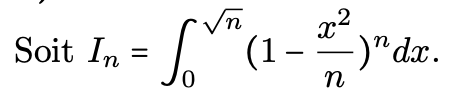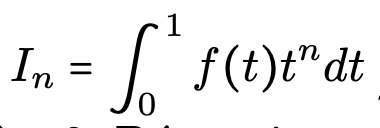Semaine 17 du lundi 2 Février : endomorphismes d’un espace euclidien
Un cours très riche qui demande un travail en profondeur :
- Définition de l’adjoint (thme-déf, il y a quelque chose à démontrer !) écriture matricielle en b.o.n.
- Si F est un s.e.v. stable par u alors son orthogonal est stable par u*.
- Donner le plus de caractérisations possibles des isométries vectorielles avec dém de l’une d’elles au choix des colleurs..
- Donner le plus de caractérisations possibles des matrices orthogonales : attention déterminant =+- 1 n’est PAS une caractérisation de ces matrices !
- Montrer qu’une matrice orthogonale symétrique est une matrice de symétrie orthogonale et montrer que vous avez compris ce que chaque terme de cette phrase veut dire….
- Théorème spectral sur les endomorphismes auto adjoints : preuve par récurrence sur la dimension (sans prouver tous les lemmes utilisés ou démo au choix parmi ces lemmes).
- Pour f dans L(E), forme bilinéaire associée (x,y)-> (x|f(y)). Par définition f est auto adjoint ssi cette forme bilinéaire est symétrique f et forme quadratique associée x-> (x|f(x)). Ecriture de ces deux objets en coordonnée dans une b.o.n. quelconque.
- Ecriture de la forme quadratique x-> (f(x)|x) dans une b.o.n. de dz. de f auto adjoint , application à une caractérisation de la plus grande et de la plus petite v.p. de f.
- Définition des autoadjoints positifs (resp. matrices symétriques positives) et caractérisation par le spectre.
- Démonstration matricielle de la forme de matrices de O_2(R)
- Théorème de réduction des isométries vectorielles en dimension n : idées de la preuve en admettant les lemmes clefs (tous assez simples à montrer par ailleursn pas besoin de formaliser la récurrence pour les blocs de rotation)
Sur la Planche-R4-2025-2026 nous avons travaillé les exercices 1 à 13 sauf le 2 et le 12.