Suites d’intégrales : convergence dominée et série d’intégrales : intégration terme à terme.
D’abord révision du programme précédent, notamment toujours soigner les justifications d’intégrabilité ou de convergence de l’intégrale, ainsi que les formules sur les primitives.
« Questions de cours » possibles :
- Citer très précisément les deux théorèmes d’intégration d’une limite (celui avec la CVU sur un segment vs le T.C.D. de Lebesgue) : lesquel sait-on démontrer 🙂 ?
- Donner un exemple d’une suite de fonctions (f_n) qui CVU sur un intervalle I (non borné) vers une fonction f et telle que l’intégrale sur I des f_n ne converge PAS vers l’intégrale sur I de f.
- Application du T.C.D. avec des « bornes variables »:

- Etude des intégrales de Wallis : détermination d’un équivalent. Toutes les étapes (relation de récurrence, invariant, encadrement) doivent être mémorisées.
- Méthode l’I.P.P fait sortir le terme prépondérant pour un équivalent
 avec hyp. f de classe C^1.
avec hyp. f de classe C^1.
- Méthode l’I.P.P fait sortir le terme prépondérant pour un équivalent
- Le même équivalent par la méthode de changement de variable.
- Intégration terme à terme d’une CVU sur un segment :
-
- application aux séries entières : (on admet la CvN sur les segments inclus dans ]-R,R[) montrer que :

- applications aux séries trigonométriques (très important car H.P. mais dans tellement de sujets d’écrits de maths et dans le cours de physique) :
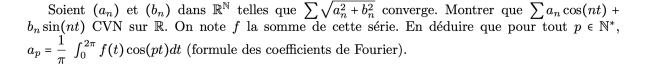
- application aux séries entières : (on admet la CvN sur les segments inclus dans ]-R,R[) montrer que :
-
- Théorème d’intégration terme à terme de Lebesgue en deux théorèmes : cas positif et cas signe quelconque. Donner des énoncés précis !
- Exemple du second cas :

- Ce qu’on fait quand le théorème ne s’applique pas. Exemple :

- Planche I2 : les exercices 1 à 5 ont été déjà faits en classe. Planche-I2-2023