Semaine 16 : du lundi 23 janvier
Thème : approximation dans les espaces de fonctions : norme infinie, norme euclidienne… et révisions, compléments de première année sur les espaces préhilbertiens.
« Question de cours » possibles :
- Citer le théorème d’approximation uniforme des fonctions c.p.m. par des fonctions en escalier et savoir l’appliquer pour démontrer le théorème de Riemann-Lebesgue sur un segment (thme H.P. mais à connaître aussi bien pour le résultat que pour la méthode).
- Citer le théorème d’approximation de Weierstrass et montrer qu’on ne peut pas espérer une CVU sur R entier car si une suite de polynômes CVU sur R entier….
- Savoir refaire la Q3 et le « lemme de Dirac » du TD : TD-Chap-T4-convolution-Weierstrass
- Espaces préhilbertiens : montrer que le produit scalaire (p.s.) est une forme bilinéaire continue.
- Exercice : lemme des moments :
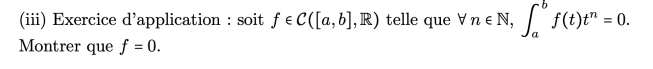
- Savoir montrer:

- Donner des exemples de sev stricts denses dans deux espaces préhilbertiens différents.
- Calcul pratique de l’orthogonalisation de Gram-Schmidt : par exemple de (1,X,X^2) pour un p.s. intégrale.
- Formule du projeté orthogonal sur F si on a une base orthogonale de F : calculs concrets.
- Théorème de meilleure approximation par le projeté orthogonal, dém (Pythagore)
- Applications concrètes de ce théorème de meilleure approximation pour la minimisation d’une intégrale…. et dans le cadre matriciel cf. Banque CCINP ex. 80, 81 et 82.
- Exercice de la Planche-T4: seuls les ex. 4,5,6,7 sont « exigibles ».