Semaine 11 : du lundi 5 décembre :
Suites d’intégrales : convergence dominée et intégration terme à terme.
D’abord révision du programme précédent, notamment toujours soigner les justifications d’intégrabilité ou de convergence de l’intégrale.
Pour les colleurs : une nouveauté cette année, le théorème d’intégration terme à terme dans le cas des intégrales de fonctions POSITIVES, avec hypothèses simplifiées (Beppo-Levi), qui simplifie donc la rédaction.
« Questions de cours » possibles :
- Exercice : Montrer que si I est BORNE et (f_n) est une suite de fonctions L^1 sur I qui CVU sur I vers une fonction f c.p.m. alors f est L^1 et la suite des intégrales des (f_n) CV vers celle de f (généralisation du théorème connu sur les segments au cas borné).
- Donner un exemple où le résultat précédent n’est PAS vrai avec I un intervalle non borné. Expliquer le problème.
- Application du T.C.D. avec des « bornes variables »:

- Etude des intégrales de Wallis : détermination d’un équivalent
- Méthode l’I.P.P fait sortir le terme prépondérant pour un équivalent (si f(1) non nul) de :

- Le même équivalent par la méthode de changement de variable.
- Intégration terme à terme d’une CVU sur un segment :
-
- application aux séries entières : montrer que :

- applications aux séries trigonométriques (très important car H.P. mais dans tellement de sujets d’écrits de maths et dans le cours de physique)
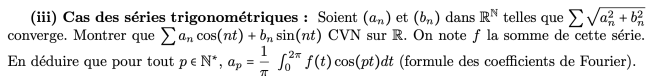
- application aux séries entières : montrer que :
-
- Théorème d’intégration terme à terme de Lebesgue en deux théorèmes : cas positif et cas signe quelconque. Exemple du second cas :

- Ce qu’on fait quand le théorème ne s’applique pas. Exemple :

- Planche I2 : les exercices 1 à 4 ainsi que le 6 ont été fait en classe cette semaine. D’autres seront corrigés lundi. Planche-I2