Un email bien sympa de Gabin, qu’il m’a autorisé à vous partager :
« Je fais suite à votre exercice qui avait une sale tête.. mais qui était en fait trop bien a faire: montrer que la matrice de Vandermonde des racines n-ieme de l’unité est inversible et calculer son inverse.
Raisonnement en deux étapes: j’ai calculé A^2, il me manquait des termes pour que ça soit beau.. puis en regardant bien la matrice on voit comment s’organisent les racines nième à l’intérieur… deux trois calculs au brouillon et non sans être guidé par les complexes et leur propriétés faites pour être utilisées ( Conjugaison ) je trouve qu’il suffit d’effectuer les calcul suivants. ( pieces jointes )
1h de casse tête, mais un casse tête agréable, d’autant plus que le résultat est trop beau pour être faux. ( j’espère ) »
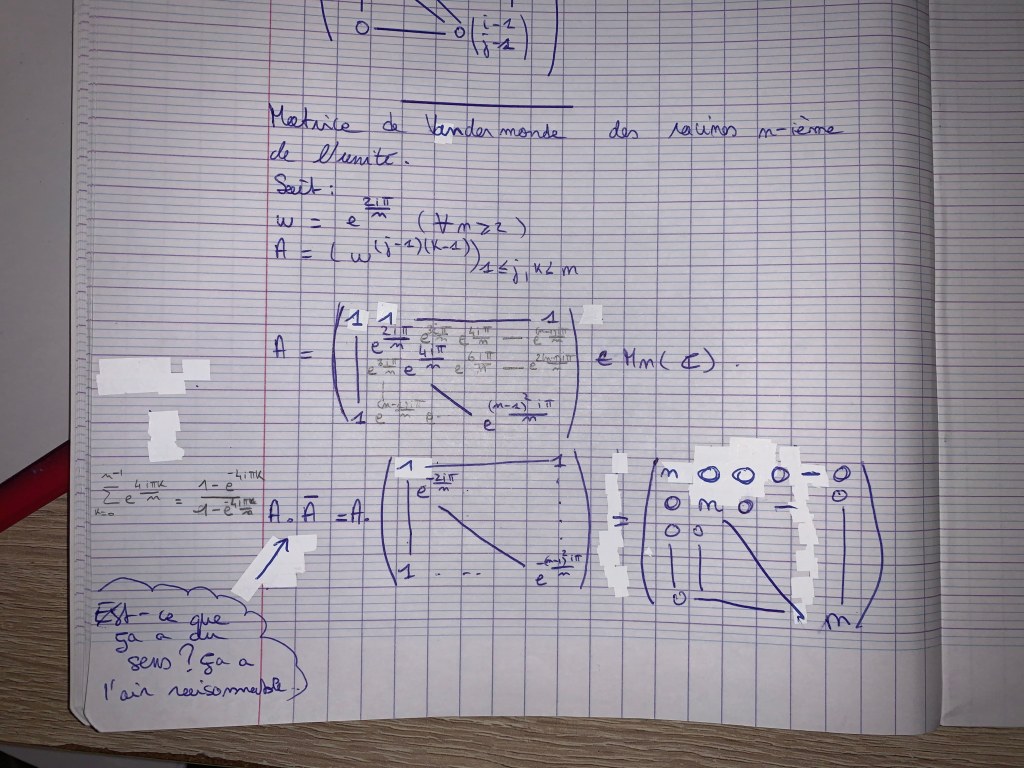

Je vous propose une seconde solution avec la même méthode qu’au tout début de la pl. 45 : faire la somme de toutes les lignes pour utiliser le fait que la somme des racines n-ièmes de l’unité fait 0.
