Bonne rédaction de Némo pour cet exercice.
Oui, il faudrait préciser la justification : e_1 est dans Ker f par la première ligne de la déf. de f et dans Imf par la seconde ligne.
Ensuite Némo fait une remarque préliminaire utile :
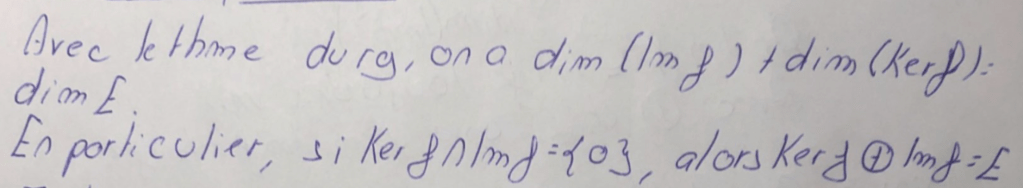
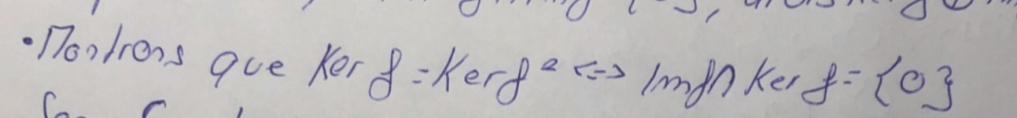
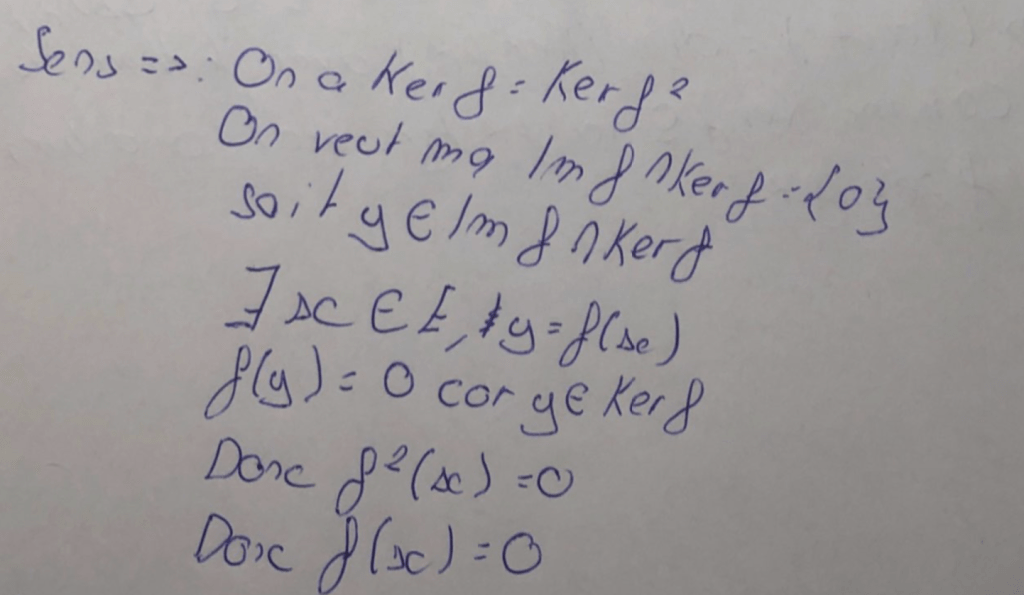
Et donc y=0.
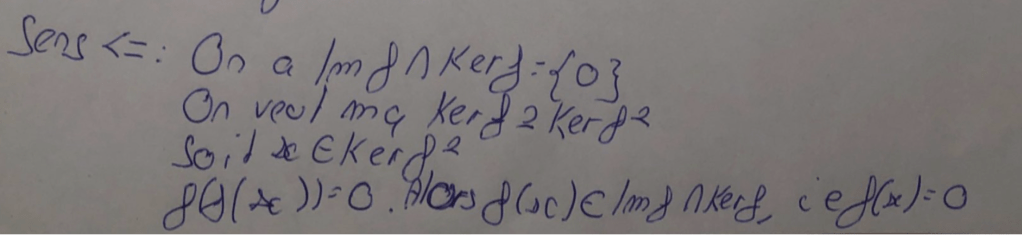
Donc x est dans Ker f, ce qui donne bien l’inclusion de Ker f^2 dans Ker f et l’autre inclusion est toujours vraie (le dire, Némo l’a dit dans une remarque préliminaire non reproduite ici).
joffremp2 